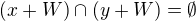Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 12. 2018 08:32
TVP - dukaz
Jak by se prosím ukázalo, že, máme§-i TVP X a platí, že pro všechna x nenulová existuje okolí bodu nula takové, že neobsahuje x, pak je X Hausdorffuv TVP.
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
- (téma jako vyřešené označil(a) Flaky)
#2 02. 12. 2018 11:33 — Editoval Sherlock (02. 12. 2018 11:35)
Re: TVP - dukaz
Pro lib. okolí nuly  existuje okolí nuly
existuje okolí nuly  t.ž.
t.ž. 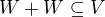 (toto plyne ze spojitosti sčítání). Zároven platí, že každé okolí nuly
(toto plyne ze spojitosti sčítání). Zároven platí, že každé okolí nuly  obsahuje podokolí nuly
obsahuje podokolí nuly  t.ž.
t.ž. 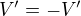 (stačí vzít
(stačí vzít 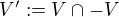 ).
).
Necht 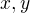 jsou 2 nenulové různé vektory.
jsou 2 nenulové různé vektory.
Nápad 1:
Nápad 2:
Nápad 3:
Finální lemma:
Snad je to dobře :D
Offline

 .
.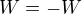 .
. okolí nuly, je
okolí nuly, je 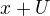 okolí bodu
okolí bodu  . To plyne z toho že zobrazení
. To plyne z toho že zobrazení 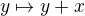 je homeomorfismus.
je homeomorfismus.