Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 12. 2018 23:45
l’Hospitalovo pravidloe
Zdravím, počítal sem sem příklady na l’Hospitalovo pravidlo a narazil sem na 3 příkladů s kterými bych potřeboval pomoci a také zkontrolovat 3 příklady které mám možná dobře ale nejsem si tím jistý:
jedná se o příklady b,c,d,g,v,xx
Takže začnu s těmi příklady , které mám možná dobře: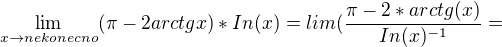
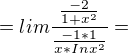


ve výsledků je taky nekonečno ,ale nejsem si jistý jestli sem k tomu výsledku došel správně
a druhý příklad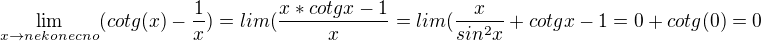
Třetí příklad na kontrolu 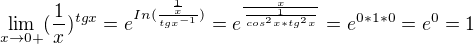
a tyto příklady nevím jak spočítat
můj postup :
poté sem to ještě zkoušel upravit ,abych tam neměl složený zlomek ,ale ani to nepomohlo, dál nevím co dělat
Další příklad 
Došel sem do této fáze dále už nevím jak postupovat, mělo by to vyjít 1
a poslední příklad 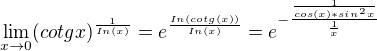
A tady sem skončil, protože nevím jak se zbavit toho X v jmenovateli a sin v čitateli.
Předem děkuji za Vaše rady
Offline
#3 03. 12. 2018 00:23
- misaH
- Příspěvky: 13459
Re: l’Hospitalovo pravidloe
↑ krakonoš:
Možno má zle iba zápis (zátvorka).
Offline
#5 03. 12. 2018 00:40 — Editoval Jarjar (03. 12. 2018 00:41)
Re: l’Hospitalovo pravidloe
↑ krakonoš: Pardon, mám tam chybu v závorce ,ale na dalším postupu to vliv nemá, alespoň doufám :D
Offline
#10 03. 12. 2018 01:21
Re: l’Hospitalovo pravidloe
↑ Jarjar:
U predposledniho bych vyuzila,ze sin(x) se chova jako x.Pak by slo o funkci x.ln(x) .Presla bych do nekonecna,takze misto x by tam bylo 1/x a uz by slo pouzit jednoduse LH pravidlo.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#11 03. 12. 2018 01:30 — Editoval Jarjar (03. 12. 2018 01:32)
Re: l’Hospitalovo pravidloe
↑ krakonoš: Děkuji moc za rady, ale ještě bych se chtěl zeptat. Moc sem nepochopil co mám špatně na tom 3. příkladu 
Offline
#13 03. 12. 2018 09:39 — Editoval krakonoš (03. 12. 2018 10:07)
Re: l’Hospitalovo pravidloe
↑ Jarjar:
Tady jsou pouzity jine upravove kroky nez vcera.Tady mi to prijde vporadku,ale efektivnejsi postup byl pouzit vcera.V poslednim kroku pred ciselnem dosazeni ma byt exponenciela umocnena na ln(tgx/x) (staci si to takto upravit).Tam ale vidim,ze je logaritmus ze x krat druha mocnina sinu.
Pri uprave ln(tgx/x) v pravem okoli nuly si staci uvedomit,ze tgx se chova jako x,protoze sinx se chova jako x.
Nebo by stacilo si vyjadrit prevracenou mocninu tg(x) pomoci sinx a cos x.A uz by ta limita byla videt. V tvem pripade se mi zda,ze jmenovatel byl zderivovan ,odpovida to derivaci cotg(x) , ale v citateli byla puvodne prevracena hodnota x,a pak je tam x.To neodpovida derivaci citatele.Takze tomuto upravovemu kroku nerozumim a nezda se mi.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#14 03. 12. 2018 15:11
Re: l’Hospitalovo pravidloe
↑ krakonoš: Aha, děkuji , ale ještě sem narazil na jeden příklad (příklad w) .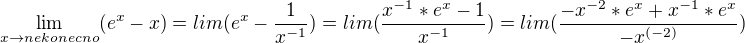
má to být takto , nebo to je špatně ? Děkuji
Offline
#15 03. 12. 2018 15:30 — Editoval krakonoš (03. 12. 2018 15:56)
Re: l’Hospitalovo pravidloe
↑ Jarjar:
Dostal jsi vyraz ((nekon/nekon) plus(nekon/nekon))/(1/nekon).Nejjednodusi bude si uvedomit,ze exponenciela v sobe obsahuje soucty vsech mocnin x,a kdyz odecteme x,vyssi mocniny zustavaji,takze to bude vysledne nekonecno.A nemusis nic pocitat.
Pokud si clovek pamatuje zpameti Tay rozvoj exponenciely,slo by to asi pouzit i u prikladu y).Prevest na spolecny jmenovatel zlomky,podelit citatele i jmenovatele x,vyuzit,ze ln(1 plus x)/x je jedna,a ze zrovnatak se ma k x inverzni funkce.A pak upravit zlomek a udelat uvahu s expone ncielou.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#18 03. 12. 2018 16:36
Offline
#19 03. 12. 2018 16:46
Re: l’Hospitalovo pravidloe
↑ jarrro:↑ jarrro[/[re]p576878:jaky prispevok?.V tech derivacich se neshodnem.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#21 03. 12. 2018 21:36 — Editoval jarrro (03. 12. 2018 21:42)
Re: l’Hospitalovo pravidloe
↑ krakonoš:išlo mi len o poukázanie na to, že
(To 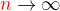 v limitách bol samozrejme preklep som to opravil)
v limitách bol samozrejme preklep som to opravil)
MATH IS THE BEST!!!
Offline
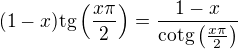
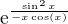 jeste jednou l'Hospital
jeste jednou l'Hospital