Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Globální extrémy funkce tří proměnných (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 12. 2018 19:01 — Editoval Al1 (09. 12. 2018 20:01)
Globální extrémy funkce tří proměnných
Dobrý den,
prosím o posunutí při hledání glob. extrémů fce  na množině
na množině ![kopírovat do textarea $M=\{[x,y,z]\in \mathbb{R}^{3}:x+y^2-z=0, x^2+y^2-16=0\}$](/mathtex/63/6321fa407bfb48983349de74e1797948.gif)
Uvnitř množiny M jsem nenašel žádné stacionární body.
Při použití Lagrangeových multiplikátorů - značím je a, b - jen pro rychlejší psaní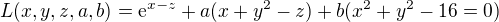
dostávám soustavu
Z druhé rovnice mám  , sečtením první a třetí mám
, sečtením první a třetí mám 
Takže dostanu


Je to správně? A pokud ano, co dál?
Děkuji za odpověď.
Offline
- (téma jako vyřešené označil(a) Al1)
#3 09. 12. 2018 20:11
Re: Globální extrémy funkce tří proměnných
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Globální extrémy funkce tří proměnných (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $[0,4,16], [0,-4,16]$](/mathtex/4c/4cf03f01ccb384601d122623d821b2ae.gif) A lze i y=0, pak
A lze i y=0, pak ![kopírovat do textarea $[4,0,4], [4,0,-4]$](/mathtex/35/35d1f0a5fb8372c4d6fb5997184a5ed9.gif) ? Všechny body mi vycházejí také při užití Jacobiho matice - to je podle zadání úlohy druhý způsob řešení, který mám také použít.
? Všechny body mi vycházejí také při užití Jacobiho matice - to je podle zadání úlohy druhý způsob řešení, který mám také použít.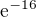 a
a  . Protoze
. Protoze ![kopírovat do textarea $y\in[-4,4]$](/mathtex/0c/0cc7cc8ddd182d8a0b2ca9e81eb61004.gif) , je
, je  a
a  ;-)
;-)