Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Funkce - rostoucí, klesající na intervalu (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 12. 2018 18:30
Funkce - rostoucí, klesající na intervalu
Zdravím,
nevím si rady s postupem k následujícímu příkladu:
Zjistit maximálně možný interval p, aby funkce byla rostoucí.
Myslel jsem si, že interval, kde je funkce rostoucí a kde klesající zjistím pomocí první derivace a pak ji položim < nebo > 0. V tomhle případě mi po zderivování zbyde pouze číslo, takže zjevně postupuji špatně.
Offline
- (téma jako vyřešené označil(a) IX)
#2 10. 12. 2018 18:36
Re: Funkce - rostoucí, klesající na intervalu
↑ IX:
Nepostupuješ špatně (když už to teda u lineární fce musíš dělat přes derivace), jen to musíš dotáhnout do konce.
Např. a) 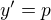 , podmínka pro rostoucí fci
, podmínka pro rostoucí fci  , takže
, takže 
ostatní obdobně
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 10. 12. 2018 18:59 — Editoval IX (10. 12. 2018 19:00)
Re: Funkce - rostoucí, klesající na intervalu
↑ zdenek1:
takže,
a) 
u b a c mi p po derivaci vypadne, znamená to tedy ž p není nijak intervalově omezeno (je tedy R) ?
Jak by se dalo řešit lineární funkce jinak než přes derivaci ?
Offline
#4 10. 12. 2018 19:03 — Editoval misaH (10. 12. 2018 19:04)
- misaH
- Příspěvky: 13460
Re: Funkce - rostoucí, klesající na intervalu
↑ IX:
Ak ide o lineárnu funkciu, jej grafom je priamka, ktorá "ide" zľava doprava nahor, teda rastie, ak pri x je kladné číslo.
Je konštantná (graf priamka rovnobežná s osou x), keď pri x je 0.
Klesá, keď pri x je záporné číslo.
Učivo ZŠ 9. ročník.
SŠ - číslo pri x je smernica priamky...
Offline
#7 10. 12. 2018 22:06
Re: Funkce - rostoucí, klesající na intervalu
↑ IX:U lineární funkce druh monotonie závisí na koeficientu u  , což je zároveň i derivace této lineární funkce, takže je jedno, jestli lineární funkci derivujeme, nebo se jen podíváme na koeficient u
, což je zároveň i derivace této lineární funkce, takže je jedno, jestli lineární funkci derivujeme, nebo se jen podíváme na koeficient u  . Pro to, aby lineární funkce byla rostoucí (myslí se tím asi ostře rostoucí, ne pouze neklesající), potřebujeme, aby koeficient u
. Pro to, aby lineární funkce byla rostoucí (myslí se tím asi ostře rostoucí, ne pouze neklesající), potřebujeme, aby koeficient u  byl kladný, takže si tuto podmínku napíšeme a pohlížíme na ni jako na nerovnici, kde neznámou je
byl kladný, takže si tuto podmínku napíšeme a pohlížíme na ni jako na nerovnici, kde neznámou je  . Zajímá nás, pro které hodnoty čísla
. Zajímá nás, pro které hodnoty čísla  nerovnost platí.
nerovnost platí.
Offline
#8 11. 12. 2018 08:43
Re: Funkce - rostoucí, klesající na intervalu
Je to funkce proměnné  s parametrem
s parametrem  . Když mluvíme o růstu nebo klesání funkce na intervalu, máme na mysli interval, odkud je proměnná
. Když mluvíme o růstu nebo klesání funkce na intervalu, máme na mysli interval, odkud je proměnná  , ale tady nás zajímá interval, odkud má být parametr
, ale tady nás zajímá interval, odkud má být parametr  , a to není interval, o kterém by se dalo říci, že na něm je funkce rostoucí nebo klesající.
, a to není interval, o kterém by se dalo říci, že na něm je funkce rostoucí nebo klesající.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Funkce - rostoucí, klesající na intervalu (TOTO TÉMA JE VYŘEŠENÉ)


 .
.