Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 01. 2019 10:14
Princip inkluze a exkluze
Ahoj potřeboval bych poradit s příkladem, kolik existuje anagramů slova SMANUNAMAS, kde vedle sebe nesmí být dvě stejná písmena.
Já si nejprve spočítal celkový počet anagramů
Poté jsem si spočítal jednu dvojičku písmenek, pokud budou vedle sebe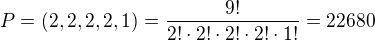
Pak dvě dvojice atd.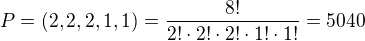



A odečetl jsem to od celkového počtu. Vyšlo mi tedy 
Je to správně?
Offline
#3 22. 01. 2019 12:22
Re: Princip inkluze a exkluze
↑ Davisek:
Jo to máš pravdu, já jsem to slovo, ale napsal špatně má to být SMANUNAMUS.
Offline

