Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 12. 2013 15:01 — Editoval dash (03. 12. 2013 15:02)
Big theta notace
Zdravím,
môžete mi prosím niekto objasniť rozdiel medzi týmito dvoma notáciami?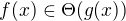
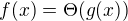
Definíciu 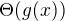 chápem ako množinu všetkých funkcii, ktoré spĺňajú podmienku
chápem ako množinu všetkých funkcii, ktoré spĺňajú podmienku  , preto mi notácia
, preto mi notácia 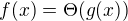 nedáva zmysel (dá sa to prečítať ako: funkčná hodnota funkcie f v bode x rovná sa množina
nedáva zmysel (dá sa to prečítať ako: funkčná hodnota funkcie f v bode x rovná sa množina 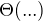 -- to je trochu nezmysel, nie?).
-- to je trochu nezmysel, nie?).
Ďakujem.
Offline
#2 03. 12. 2013 15:39
Re: Big theta notace
↑ dash:
Zdravím.
Rigorosním zápisem je 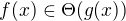 , zatímco zápis
, zatímco zápis 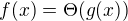 (mající znamenat totéž) je pouze mnemotechnický
(mající znamenat totéž) je pouze mnemotechnický
pro pohodlnější provádění výpočtů, například
 pro
pro 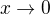 ,
,
ale já jsem nikdy neměl potřebu používat tuto notaci a nemám s ní mnoho zkušeností, takže někdo možná příjde s lepším příkladem.
Offline
#3 03. 12. 2013 16:15 — Editoval vanok (03. 12. 2013 16:16)
Re: Big theta notace
Ahoj,
Precitaj si aj toto.
http://en.wikipedia.org/wiki/Big_O_notation
Osobne naviac pouzivam O, o, a ekvivalenciu.
Iste sa pouzivaju aj ine znacenia, a iste ti tu niekto o tom napise.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 27. 01. 2019 12:21 — Editoval slender (27. 01. 2019 12:23)
Re: Big theta notace
Pro případné další kolemjdoucí, co si stejně jako já chtějí udělat pořádek v notacích a narazí na toto vlákno, na české Wikipedii je pěkná tabulka popisující jednotlivé óčkové a omegové notace (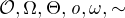 ).
).
Offline
#5 30. 01. 2019 11:57
Re: Big theta notace
Ahoj ↑ slender:,
Len pre upresnenie, tvoj odkaz je ten isty ako moj ↑ vanok:. Moj odkaz je anglicka ( podrobnejsia) verzia a tiez je uzitocne si pozriet aj francuzku verziu. Ceska verzia je o mnoho skromnejsia.
Dovolim si pripomenut, ze je na tuto temu vediet aspon, ze
Dve realne funkcie 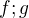 definovane a nenulove v okoli bodu
definovane a nenulove v okoli bodu  ( ineho ako a) maju zaujimave vlasnosti, podla toho, ze
( ineho ako a) maju zaujimave vlasnosti, podla toho, ze 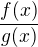 pre
pre 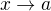 v tycto pripadoch:
v tycto pripadoch:
1)
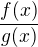 je ohranicena v okoli
je ohranicena v okoli 
Co sa povie, ze g dominuje f
Piseme 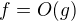
2)
Povieme, ze f je nepatrna pred g ( v okoli a):
Ak 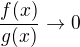 pre
pre 
Co piseme 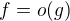
3)
Povieme, ze f a g su ekvivalentne ( v okoli a):
Ak 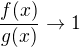 pre
pre 
Piseme 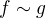 .
.
O ich pouziti som uz tu na fore vela popisal.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
