Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Fyzika
- » Magnetické pole generované dodatečným proudem (TOTO TÉMA JE VYŘEŠENÉ)
#26 10. 02. 2019 10:32
Re: Magnetické pole generované dodatečným proudem
Celá tvá argumentace stojí jen na tom, že máme v úloze místa, kde funkce nejsou diferencovatelné.
Jako fyzik by sis měl s takovou drobností poradit. Jedna z možností je si představit situaci, kde vše diferencovatelné bude, a přitom bude libovolně blízká naší situaci. Můžeš si to představit taky jako posloupnost takovýchto situací, které se (v limitě) blíží k té naší nespojité.
A nebo můžeš využít Diracových funkcí, to se také běžně dělá - dokonce to má i svůj název, metoda Greenových funkcí.
Stavět argumetnaci jen na tomhle je asi podobné, jako tvrdit, že Coulombův zákon neplatí, protože pro bodový náboj nemá rovnice řešení.
Ještě tam zmiňuješ, že na povrchu vodiče neexistuje E, proč by tam nemělo existovat? Jen se nespojitě mění z nuly na nenulu...
A pak ještě jedna věc (i když s naším problémem to úplně nesouvisí) - tvůj "výpočet B z Maxwellových rovnic" není jen z Maxwellových rovnic, ale ještě ze symetrie úlohy, z toho, že je úloha symetrická kolem nějaké osy. V žádném jiném případě by se takový výpočet nedal aplikovat, protože když známe rot B, nestačí to k tomu, abychom B určili jednoznačně. Takže tvá argumentace by v důsledku vedla k tomu, že v jiných než symetrických případech magnetické pole nedokážeme určit vůbec (a tedy asi neexistuje) - protože jsou tam ty místa, kde funkce nejsou diferenciovatelné a tudíž rovnice nelze řešit, a princip symetrie použít nemůžeme.
Né, to že někde nelze určit derivace není chyba rovnic, ani přírody, ale jen našeho zjednodušeného modelu, který jsme si zjednodušili až přespříliš. A pak si s tím buď nějak dokážeme poradit, nebo né (a měli bychom si tedy najít lepší model). Ale dělat na základě toho nějaké úvahy o skutečném světě, myslím na základě toho, že v našem modelu nelze počítat derivace, to je nesmysl.
Offline
#27 10. 02. 2019 10:36 — Editoval MichalAld (10. 02. 2019 20:10)
Re: Magnetické pole generované dodatečným proudem
Dotaz ohledně řešení LaPlaceovy rovnice vložím do matematické části fóra, třeba to někdo ví z hlavy. Já si třeba pamatuji větu, že pokud máme (pro LaPlaceovu rovnici) stanoveny hodnoty na okraji nějaké oblasti, tak uvnitř oblasti jsou její hodnoty vždy mezi tím, co je na okraji.
Nakonec, LaPlaceova rovnice určuje třeba rozložení teploty v tělese, pokud známe teplotu na jejím povrchu. Takže si představ třeba krychli, na jejíchž stěnách drříme nějaké konstantní teploty, a ptáme se na teplotu uvnitř (v ustáleném stavu). I bez počítání se zdá být extrémně nepravděpodobné, že by teplota uvnitř krychle měla být vyšší než na jejich stěnách.
Pokud na stěnách krychle budeme držet nulovou teplotu, těžko se uvnitř vytvoří větší. A je jedno, jak velká krychle bude, takže si ji můžeme představit i nekonečně velkou.
No a stejné rovnice mají i stejná řešení, takže když to platí pro teplotu, platí to i pro elektrický potenciál, i pro složky vektoru magnetického pole.
Tvrzení ohledně Laplaceovy rovnice lze případně rozporovat tady.
Offline
#28 10. 02. 2019 11:01 — Editoval MichalAld (10. 02. 2019 13:24)
Re: Magnetické pole generované dodatečným proudem
KennyMcCormick napsal(a):
Edit: Tam by mě zajímalo, jak by se měnila ta hustota náboje na deskách, pokud by výsledné
bylo spojité a jak to je v souladu s tím, že se dá ukázat, že náboj bude pouze v nekonečně tenké vrstvě na povrchu. (Možná je nějaká hlubší analýza, která ukazuje, že je to možné, nebo to souvisí s tím, že se elektrické pole mění v čase... (Nemohou to být ale elektrony, protože elektrony představují v klasickém elektromagnetismu nespojitost
.))
Pokud jde o tohle, je to zase jen zjednodušená představa "ideálního vodiče" - tentokrát není ideální v tom, že by měl nulový odpor, ale je ideální v tom, že to fluidum, co nese náboj a při svém pohybu vytváří proud, ať už je to co chce, tak nezabírá žádný objem.
Jinak řečeno, mezi elementy q nepůsobí žádná jiná síla než elektrická.
Takže v našem vodiči, pokud by tam nějaké náboje byly, bude tam i elektrické pole (opět naše oblíbená Poissonova/Laplaceova rovnice) a toto pole nám uvede náboje do pohybu (protože v našem ideálním vodiči není nic, co by je zadrželo, jen hranice toho vodiče).
Pokud ale vezmeme reálnější model, kde elementy náboje q budou zabírat i elementární objem v, dojdeme k tomu, že už nebudou rozloženy v nekonečně tenké vrstvě, nýbrž ve vrstvě konečné tloušťky d, a intenzita E se nebude měnit skokem, nýbrž spojitě.
Všechno jsou to samozřejmě zjednodušení, která používáme, abychom se něčeho dobrali. Co dělají skutečné elekrony bychom museli určit z kvantové mechaniky - a pak vzít pravděpodobnost, kterou nám kvantovka předpoví, jako hustotu kterou potřebujeme v klasických rovnicích. Je ale celkem jisté, že elektrony nebudou v nekonečně tenké vrstvě (atomy také nejsou nekonečně malé).
PS: ono je také dobré mít pořád na paměti, že Maxwellovy rovnice jsou opravdu fundamentální fyzikou (myslím ty Maxwellky bez H a D), jejich platnost končí až tam, kde začíná kvantová mechanika. Zatímco ty "materiálové rovnice" to je úplně někde jinde - to jsou zpravidla jen takové velmi zjednodušené modely toho, jak se látky chovají, a mají vždy dost omezenou platnost.
Dokonce je to tak, že Maxwellovy rovnice pole (tedy bez těch zdrojů, nábojové a proudové hustoty) zůstávají stejné i v kvantové mechanice. Jen se tam používá ta varianta rovnic s elektrickým a magnetickým potenciálem, a né ta s E a B. Jsou ale ekvivalentní (stejné rovnice mají i stejná řešení)...jen se v kvantovce jinak používají a hlavně jinak interpretují. Tohle né každý ví - že kvantové odlišnosti se týkají především elektronů (či jiných nabitých částic) a jejich interakcí s el. mag. polem. Co se týká samotných fotonů, žádné nové věci kvantovka nepřináší, jen samotnou existenci těch fotonů (která plyne z toho, jak se rovnice interpretují). Ale vlastní el. mag. pole či vlny jsou v kvantovce víceméně stejné jako v klasické teorii.
Offline
#29 11. 02. 2019 04:56 — Editoval KennyMcCormick (11. 02. 2019 05:07)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Magnetické pole generované dodatečným proudem
Celá tvá argumentace stojí jen na tom, že máme v úloze místa, kde funkce nejsou diferencovatelné.
Celá ne, v případě situace 2 jsem psal
Nemůžeme použít Liouvilleovu větu, protože
není omezená.
 utíká do nekonečna pro
utíká do nekonečna pro 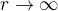 .
.
(Tam jsem ještě mohl připsat, že by nebyla splněna Maxwellova rovnice, protože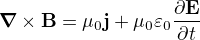 by se rovnalo
by se rovnalo . (A totéž platí i v situaci 3)
. (A totéž platí i v situaci 3)
Stavět argumetnaci jen na tomhle je asi podobné, jako tvrdit, že Coulombův zákon neplatí, protože pro bodový náboj nemá rovnice řešení.
Pro 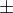 bodový náboj
bodový náboj  . 🙂
. 🙂
Ještě tam zmiňuješ, že na povrchu vodiče neexistuje E, proč by tam nemělo existovat? Jen se nespojitě mění z nuly na nenulu...
Protože potenciál je uvnitř konstantní a v místě povrchu směrem ven náhle začíná klesat tak, že v bodě povrchu je nediferencovatelný (takže tam není definovaná normálová složka elektrické intenzity). (Otázka je, jestli existuje nějaké rozložení nábojů, pro které ten potenciál klesá diferencovatelně...)
↑ MichalAld:
"výpočet B z Maxwellových rovnic" není jen z Maxwellových rovnic, ale ještě ze symetrie úlohy, z toho, že je úloha symetrická kolem nějaké osy. V žádném jiném případě by se takový výpočet nedal aplikovat, protože když známe rot B, nestačí to k tomu, abychom B určili jednoznačně
Ano. Schválně jsem to zjednodušil na symetrickou situaci, aby se to lépe počítalo. Ale ani v nesymetrické situaci by konstantní posuvný proud nevytvořil nulové magnetické pole.
↑ MichalAld:
Pokud ale vezmeme reálnější model, kde elementy náboje q budou zabírat i elementární objem v, dojdeme k tomu, že už nebudou rozloženy v nekonečně tenké vrstvě
Jestli myslíš náboje, které představují rovnoměrnou objemovou hustotu náboje v určitém prostoru, nerozletěl by se každý takový elementární náboj na kousky?
(Kdyby to byla spojitá nábojová hustota (a ne elementární náboje složené z rovnoměrné nábojové hustoty), tak by se soutředila v nekonečně tenké vrstvě na povrchu vodiče (aspoň myslím, že odvození, že pod povrchem vodiče nemůže existovat ve stacionární situaci náboj, se nespoléhá na to, že jsou to individuální elektrony(?)))
Jedna z možností je si představit situaci, kde vše diferencovatelné bude, a přitom bude libovolně blízká naší situaci.
Taková situace není fyzikálně možná. 🙂
Důkaz sporem: Nechť existuje takové rozložení 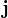 a
a 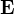 , že
, že 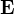 je všude spojité, posuvný proud je konstantní v čase a
je všude spojité, posuvný proud je konstantní v čase a  v každém bodě prostoru. Taky předpokládejme, že
v každém bodě prostoru. Taky předpokládejme, že  , a že tedy (pokud ten důkaz v odkazovaném vlákně platí i pro vektorový Laplacián)
, a že tedy (pokud ten důkaz v odkazovaném vlákně platí i pro vektorový Laplacián) 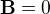 ve všech bodech v prostoru. A předpokládejme, že náš posuvný proud negeneruje magnetické pole.
ve všech bodech v prostoru. A předpokládejme, že náš posuvný proud negeneruje magnetické pole.
Maxwellova rovnice: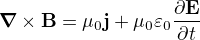 , tj.
, tj. v každém bodě prostoru.
v každém bodě prostoru.
V každém bodě prostoru tedy platí, že hustota posuvného proudu je rovna záporné hustotě vodivého proudu a obě hustoty jsou konstantní.
Taková situace nemůže nastat, protože konstantní vodivý proud vyžaduje konstantní 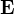 v každém svém bodě (buď nulovou, pokud je to ideální vodič, nebo nenulovou pro vodič s odporem), což je spor.
v každém svém bodě (buď nulovou, pokud je to ideální vodič, nebo nenulovou pro vodič s odporem), což je spor.
(Ani Liouvilleovu větu nemůžeme použít: Nechť existuje takové rozložení 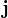 a
a 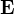 , že
, že 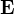 je všude spojité, posuvný proud je konstantní v čase,
je všude spojité, posuvný proud je konstantní v čase, 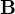 je celá funkce a
je celá funkce a  a tím pádem
a tím pádem 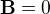 v každém bodě prostoru, zbytek důkazu by byl stejný.)
v každém bodě prostoru, zbytek důkazu by byl stejný.)
Takže ani jeden z těch dvou nápadů nefunguje.
Je otázka, co zbývá. Mohli bychom říct, že nás zajímají jenom situace, kde 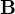 je nenulová alespoň v jednom bodě prostoru a zároveň je tam posuvný proud uspořádaný tak, že se všechny jeho příspěvky k magnetickému poli navzájem ruší. (A ta nenulová oblast magnetického pole by pak byla způsobená vodivým proudem.) Otázkou je, jestli takové rozložení existuje a jak ho najít. (Nemůže to být situace při nabíjení/vybíjení kondenzátoru, protože tam se proud zachovává, takže magnetické pole mezi deskami je stejné jako uvnitř vodiče, protože posuvný proud vyvolává přesně stejné magnetické pole jako vodivý.)
je nenulová alespoň v jednom bodě prostoru a zároveň je tam posuvný proud uspořádaný tak, že se všechny jeho příspěvky k magnetickému poli navzájem ruší. (A ta nenulová oblast magnetického pole by pak byla způsobená vodivým proudem.) Otázkou je, jestli takové rozložení existuje a jak ho najít. (Nemůže to být situace při nabíjení/vybíjení kondenzátoru, protože tam se proud zachovává, takže magnetické pole mezi deskami je stejné jako uvnitř vodiče, protože posuvný proud vyvolává přesně stejné magnetické pole jako vodivý.)
(Nemůžeme přeskakovat ověření předpokladů - např. kdybychom uvažovali podmínku, že v nekonečnu jde 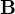 k nule a přepokládali, že je holomorfní v celém prostoru (a zároveň omezená), pak dojdeme k tomu, že
k nule a přepokládali, že je holomorfní v celém prostoru (a zároveň omezená), pak dojdeme k tomu, že 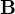 je vždycky nula v celém prostoru za všech okolností (Liouvilleova věta), což není pravda.) 🙂
je vždycky nula v celém prostoru za všech okolností (Liouvilleova věta), což není pravda.) 🙂
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#31 11. 02. 2019 15:48
Re: Magnetické pole generované dodatečným proudem
KennyMcCormick napsal(a):
Ještě tam zmiňuješ, že na povrchu vodiče neexistuje E, proč by tam nemělo existovat? Jen se nespojitě mění z nuly na nenulu...
Protože potenciál je uvnitř konstantní a v místě povrchu směrem ven náhle začíná klesat tak, že v bodě povrchu je nediferencovatelný (takže tam není definovaná normálová složka elektrické intenzity). (Otázka je, jestli existuje nějaké rozložení nábojů, pro které ten potenciál klesá diferencovatelně...)
Pro jakékoliv "rozumné" prostorové rozložení náboje, tj. takové, které lze popsat téměř libovolnou 3D funkcí, se výsledná intenzita mění spojitě.
Aby se měnila nespojitě, museli bychom rozložení náboje v prostoru popsat zase pomocí nějakých "Diraců". A představa, že se nám nějaké 3D objekty (jako třeba elektrony) vtěstnají do množiny nulové míry (vůči prostoru, tedy do plochy, čáry, bodu) je v reálném světě nesmysl. Je to zase jen nějaká naše velmi zjednodušená představa.
V reálném světě je všechno spojité a diferencovatelné, funkce co nemají derivaci jsou jen v matematice. Protože jsou jednoduché...
Offline
#32 11. 02. 2019 15:53 — Editoval MichalAld (11. 02. 2019 15:55)
Re: Magnetické pole generované dodatečným proudem
KennyMcCormick napsal(a):
Jedna z možností je si představit situaci, kde vše diferencovatelné bude, a přitom bude libovolně blízká naší situaci.
Taková situace není fyzikálně možná. 🙂
Důkaz sporem: Nechť existuje takové rozloženía
, že
je všude spojité, posuvný proud je konstantní v čase a
v každém bodě prostoru. Taky předpokládejme, že
, a že tedy (pokud ten důkaz v odkazovaném vlákně platí i pro vektorový Laplacián)
ve všech bodech v prostoru. A předpokládejme, že náš posuvný proud negeneruje magnetické pole.
Trochu se do toho zamotáváte, pane. Nechápu, kde jsi vzal, že máme předpokládat spojité j, a zároveň
Musíme přece předpokládat, že 
Mícháš dohromady Laplaceovu a Poissonovu rovnici. Nulové B v celém prostoru jako jediné nedivergující řešení platí jen pro tu Laplaceovu. Pokud má pravou stranu, tak to samozřejmě neplatí.
Offline
#34 11. 02. 2019 17:00
Re: Magnetické pole generované dodatečným proudem
Můžeme také předpokládat, že
No a ten druhý člen je v našem případě nulový. O tom tu pořád mluvíme.
A jediný argument, který proti tomu máš, je že záměnu derivací nelze provést ... protože ty funkce nejsou dostatečně hladké.
Offline
#35 11. 02. 2019 18:03
Re: Magnetické pole generované dodatečným proudem
KennyMcCormick napsal(a):
Jestli myslíš náboje, které představují rovnoměrnou objemovou hustotu náboje v určitém prostoru, nerozletěl by se každý takový elementární náboj na kousky?
(Kdyby to byla spojitá nábojová hustota (a ne elementární náboje složené z rovnoměrné nábojové hustoty), tak by se soutředila v nekonečně tenké vrstvě na povrchu vodiče (aspoň myslím, že odvození, že pod povrchem vodiče nemůže existovat ve stacionární situaci náboj, se nespoléhá na to, že jsou to individuální elektrony(?)))
Tohle je celkem základní věc - síly, které dokáží udržet náboj na nějakém konkrétním místě v prostoru (jako třeba na povrchu vodiče) nemohou být elektrické povahy. Musejí to být nějaké jiné síly. Samotná klasická teorie elektromagnetismu nedokáže vysvětlit, že jsou atomy (či látka jako celek) stabilní.
Lze ukázat, že jakákoliv konfigurace bodových nabitých částic je nestabilní, a buď by se měla rozletět do nekonečna, nebo smrštit do nekonečně malého bodu. Elektrostatika (ani elektrodynamika) nemá nic, co by tomu zabránilo. Atomy, a tím pádem ani stavbu látek, nelze pomocí Maxwellových rovnic vůbec vysvětlit.
Pak je tu ještě jedna věc - to že používáme rovnice pole, které používají spojité veličiny (jako nábojovou či proudovou hustotu) vůbec nemusí znamenat, že je to tak i ve skutečnosti. Znamená to pouze, že řešíme problémy, jejichž rozměry jsou mnohem větší, nežli je struktura skutečné hmoty. Máš to podobné, jako s tou teplotou - také můžeme předpokládat v každém bodě určitou teplotu - a přitom je to blbost, protože měřit teplotu v levé a pravé části nějakého atomu se nám těžko podaří. U proudící tekutiny také předpokládáme spojité rozložení rychlosti - a nemyslíme tím rychlosti jednotlivých molekul (ty mají třeba i svůj tepelný pohyb). Nakonec ten tepelný pohyb nezohledňujeme (zpravidla) ani u el. proudu - pokud nás zrovna nezajímá Johnsonův šum...
Offline
#36 11. 02. 2019 18:14
Re: Magnetické pole generované dodatečným proudem
Ještě jsem si třeba vzpoměl - pokud jde o představu "bodového náboje složeného z nábojové hustoty" - tak to je ve skutečnosti kámen úrazu elektromagnetické teorie.
Lze totiž definovat něco jako je elektromagnetická hmotnost. Vychází se z představy, že el. mag. pole, které pohybující se částice vytváří, může působit zpětně i na tu částici, co jej vytvořila. Jenže v limitě, pro nekonečně malou částici, vychází tato síla nekonečná. Bodový náboj by měl mít tedy nekonečnou hmotnost.
Pak se nabízí představa, že částice má jen konečnou velikost - že je to nějaká kulička vhodně "potažená" nábojovou hustotou. Jenomže tady je zase problém, co tu nábojovou hustotu drží pohromadě (měla by se rozletět). A má to dost hluboké důsledky - protože tahleta hmotnost se netransformuje správně při Lorentzově transformaci. Prostě ta energie, co to drží pohromadě, tam chybí.
Navíc - o podstatě téhle neelektrické síly, co by držela nábojovou hustotu na kuličce nemá nikdo nejmenší představu.
A problém nezmizí ani v kvantové mechanice. Tam elektron také považujeme za bod, ale při počítání nějakého QED výpočtu se (prý) musí skončit v nějaké konečné vzdálenosti. Jinak to (prý) také diverguje.
Bodové náboje jsou tedy v jistém smyslu v rozporu s klasickou el. mag. teorií. Tenhle problém nebyl nikdy uspokojivě vyřešen.
Offline
#37 11. 02. 2019 18:49 — Editoval KennyMcCormick (11. 02. 2019 19:41)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Magnetické pole generované dodatečným proudem
↑ MichalAld:
Nebo tak.
↑ MichalAld:
Nechápu, kde jsi vzal, že máme předpokládat spojité j, a zároveň
Přepokládáš, že všechno je spojité, takže i 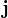 je spojité. A předpokládáš, že
je spojité. A předpokládáš, že  v každém bodě prostoru v tom vedlejším vlákně.
v každém bodě prostoru v tom vedlejším vlákně.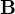 v Maxwellových rovnicích není
v Maxwellových rovnicích není 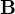 generované určitým proudem. Je to
generované určitým proudem. Je to 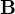 v daném bodě prostoru.
v daném bodě prostoru.
V tomhle případě si to nemůžeme rozdělit na posuvný a vodivý proud, protože každý případ zvlášť neřeší Maxwellovy rovnice (přestože součet obou případů je splňuje) (a to nesouvisí se spojitostí/nespojitostí funkcí). Platí, že součet řešení řeší Maxwellovy rovnice. Neplatí, že pro jakoukoliv dekompozici řešení je i každá část řešením. (Ze stejného důvodu, proč pro  ležící na přímce
ležící na přímce  i
i  ležící na přímce
ležící na přímce  platí, že
platí, že 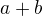 leží na přímce
leží na přímce  , ale kdybych to chtěl udělat obráceně - tj. kdybych začal s bodem
, ale kdybych to chtěl udělat obráceně - tj. kdybych začal s bodem  ležícím na přímce
ležícím na přímce  a chtěl ho vyjádřit jako nějaký součet bodů
a chtěl ho vyjádřit jako nějaký součet bodů 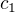 a
a  , tak nemůžu automaticky předpokládat, že libovolné body
, tak nemůžu automaticky předpokládat, že libovolné body 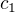 a
a  budou ležet na přímce
budou ležet na přímce  ).
).
(Dává to takhle smysl?)
(Jinak, jestli mi nevěříš ten obecný princip (že když chceš Maxwellovy rovnice řešit tak, že zadání rozdělíš do dvou částí, obě řešení pak sečteš a získáš výsledné řešení, že si musíme nejdřív zkontrolovat, že každá část sama o sobě vyhovuje Maxwellovým rovnicím), tak si založíme vlákno na Physics StackExchange a zeptáme se tam, abys mi věřil.)
↑ MichalAld:
síly, které dokáží udržet náboj na nějakém konkrétním místě v prostoru (jako třeba na povrchu vodiče) nemohou být elektrické povahy
To můžeme - postulovat, že existují síly, které tu objemovou hustotu náboje drží pohromadě. Takže elektron bude koule vyplněná rovnoměrnou objemovou nábojovou hustotou. Taková objemová hustota by nebyla ani ta obyčejná nábojová hustota (protože ta by byla v nekonečně tenké vrstvě na povrchu vodiče), ani klasický elektron (protože to je bod), ani semiklasický (protože to je koule s nábojem na povrchu a žádným nábojem uvnitř).
Takže, když se to udělá takhle, tak se dojde k přesnějším výsledkům?
(Ale samozřejmě vím, že statické rozložení nábojů nemůže být držené pohromadě jenom elektrickými silami.) 🙂
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#38 11. 02. 2019 20:54 — Editoval MichalAld (11. 02. 2019 20:54)
Re: Magnetické pole generované dodatečným proudem
KennyMcCormick napsal(a):
Nechápu, kde jsi vzal, že máme předpokládat spojité j, a zároveň
Přepokládáš, že všechno je spojité, takže i
je spojité. A předpokládáš, že
v každém bodě prostoru v tom vedlejším vlákně.
v Maxwellových rovnicích není
generované určitým proudem. Je to
v daném bodě prostoru.
Ale né, to je velké nedorozumění. Já nepředpokládám, že  , jde o to, že když je
, jde o to, že když je  tak je také B = 0.
tak je také B = 0.
Takže když předpokládám, že 
jako například 
a to něco na pravé straně bude nula, tak z toho plyne, že B = 0.
Offline
#39 11. 02. 2019 21:02
Re: Magnetické pole generované dodatečným proudem
Dále - já předpokládám, že víš, jak vypadá řešení Poissonovy rovnice (tj té s pravou stranou). Ale pokud né - je to takto:
kde P je nějaká téměř libovolná funkce, tak řešení lze ziskat jako součet funkcí P(x,y,z)/r přes všechny možné body x,y,z. Je to přesně to, co v elektrostatice známe jako potenciál bodového náboje. Takže každý bod, kde je funkce P nenulová, přispěje k celkovému potenciálu svým příspěvkem P()/r, kde r je samozřejmě 
To je to, čemu říkám "příspěvek k celkovému poli.
U magnetického pole to funguje úplně stejně. Také jsi se ptal, když to bude vektorová a né skalární rovnice. Ale je to to samé, pro každou složku vektoru zvlášť.
Offline
#40 11. 02. 2019 21:09
Re: Magnetické pole generované dodatečným proudem
KennyMcCormick napsal(a):
V tomhle případě si to nemůžeme rozdělit na posuvný a vodivý proud, protože každý případ zvlášť neřeší Maxwellovy rovnice (přestože součet obou případů je splňuje) (a to nesouvisí se spojitostí/nespojitostí funkcí). Platí, že součet řešení řeší Maxwellovy rovnice. Neplatí, že pro jakoukoliv dekompozici řešení je i každá část řešením.
Tohle je (alespoň do jisté míry) určitě pravda - píše to nakonec i Feynman.
A pokud považujeme za výchozí rovnice ty běžně známé
rot B = ...
div B = ...
tak to dodržovat musíme.
Pokud ovšem za výchozí rovnici budeme považovat tu
a za odvozené ty prvně zmíněné, nic nás nenutí se těmi "prvními" zabývat. A těm "druhým" to nevadí - protože tam obě části řešení rovnici splňují.
Jasně, je to trochu uhozené začít považovat za fundamentální jinou rovnici, než co je běžně zvykem. Na druhou stranu, kvantova už jednoznačně považuje za fundamentální rovnice napsané v elektromagnetickém potenciálu (a vysoká teoretická klasická fyzika nakonec taky) - a ty se podobají spíš té "druhé" rovnici než těm "prvním". A rovnice napsané v potenciálech neobsahují ten posuvný proud vůbec. Respektive je tam schovaný v tom magnetickém potenciálu - v té jeho části, která se fyzikálně neprojevuje. Časem se k tomu dostanu.
Offline
#41 11. 02. 2019 21:20
Re: Magnetické pole generované dodatečným proudem
Ještě to zkusím napsat jinak. Pokud použijeme tuhle rovnici,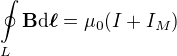
tak tam ten posuvný proud mít musíme. Jinak se samozřejmě dostaneme do sporu, protože výsledek by závisel na tom, jak si zvolíme tu plochu, ohraničenou křivkou L.
Jenže tohle je prostě integrální rovnice. Neříká nám nic o tom, která nabitá částice nám jakou měrou přispívá k magnetickém poli v místě, kde ho počítáme.
Jenomže to je zcela korektní otázka. Celkové magnetické (elektromagnetické) pole musí jít v principu spočítat i tak, že spočteme dílčí el. mag. pole tvořené každou nabitou částicí, co v situaci máme (mag pole tvořené každým pohybujícím se elektronem) a jednotlivé příspěvky sečteme.
A zde se naskýtá jednoduchá otázka - stačí sečíst jen příspěvky od pole tvořené jednotlivými elektrony ? Nebo musíme vzít ještě nějaké jiné příspěvky ? (od toho posuvného proudu) ?
No a ta druhá rovnice na to svým způsobem odpovídá.
Offline
#42 11. 02. 2019 21:43
Re: Magnetické pole generované dodatečným proudem
KennyMcCormick napsal(a):
Takže elektron bude koule vyplněná rovnoměrnou objemovou nábojovou hustotou. Taková objemová hustota by nebyla ani ta obyčejná nábojová hustota (protože ta by byla v nekonečně tenké vrstvě na povrchu vodiče), ani klasický elektron (protože to je bod), ani semiklasický (protože to je koule s nábojem na povrchu a žádným nábojem uvnitř).
Ta "obyčejná nábojová hustota" - co se vyskytuje v Maxwellových rovnicích, to je právě ta objemová.
Stejně tak vektor proudové hustoty j je objemová hustota proudu.
Pokud jde o elektron, můžeme si představit libovolné množství způsobů, jak je nábojová hustota rozložena kolem jeho středu. Nemusí to být zrovna jen "rovnoměrně vyplněná koule".
Vzhledem k tomu že víme, kolik elektron váží a jaká energie je potřeba na vytvoření příslušného el. pole, lze definovat něco jako klasický poloměr elektronu. A lze samozřejmě vymýšlet i jiná rozložení náboje - pak se vypočtená velikost liší v řádu o nějakou malou konstantu, asi jako při výpočtu momentů setrvačnosti.
Offline
#43 11. 02. 2019 22:54 — Editoval KennyMcCormick (11. 02. 2019 22:55)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Magnetické pole generované dodatečným proudem
Pokud ovšem za výchozí rovnici budeme považovat tu
a za odvozené ty prvně zmíněné
Z toho Maxwellovy rovnice neodvodíš.
↑ MichalAld:
Pokud použijeme tuhle rovnici,
tak tam ten posuvný proud mít musíme. Jinak se samozřejmě dostaneme do sporu, protože výsledek by závisel na tom, jak si zvolíme tu plochu, ohraničenou křivkou L.
Jenže tohle je prostě integrální rovnice. Neříká nám nic o tom, která nabitá částice nám jakou měrou přispívá k magnetickém poli v místě, kde ho počítáme.
Říká nám, že proudy, které procházejí plochou vymezenou tou smyčkou, přispívají k cirkulaci magnetického pole. Takže, pokud posuvný proud tou plochou prochází, tak přispívá k cirkulaci.
↑ MichalAld:
Ta "obyčejná nábojová hustota" - co se vyskytuje v Maxwellových rovnicích, to je právě ta objemová.
Stejně tak vektor proudové hustoty j je objemová hustota proudu.
Já vím. 🙂
Vzhledem k tomu že víme, kolik elektron váží a jaká energie je potřeba na vytvoření příslušného el. pole, lze definovat něco jako klasický poloměr elektronu.
Ano, ale to by byl elektron s plošnou nábojovou hustotou na svém povrchu, což nechceš (protože jsi psal, že se objemová nábojová hustota mění spojitě). Zase na druhou stranu, věřím ti, že Diracova zobecněná funkce ti umožní spojité změny 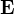 i v bodových nábojích. (Nestačí to k tomu, aby bylo definované úplně všechno a aby bylo všechno spojité, ale to v kontextu intenzity na okraji vodiče nevadí.)
i v bodových nábojích. (Nestačí to k tomu, aby bylo definované úplně všechno a aby bylo všechno spojité, ale to v kontextu intenzity na okraji vodiče nevadí.)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#44 12. 02. 2019 00:54
Re: Magnetické pole generované dodatečným proudem
KennyMcCormick napsal(a):
Z toho Maxwellovy rovnice neodvodíš.
Jak to víš ?
Já bych naopak řekl, že skoro jo....
Každopádně je odvodím z tohoto:

A pro B platí prostě 
Ten "čtvereček" je d'Alemberův operátor, ale to asi víš.
Ale hlavně - to j na pravé straně rovnice je jen skutečná proudová hustota, nezahrnuje žádný "posuvný proud".
Za podmínek o kterých mluvíme, tj 2. derivace podle času je nulová, nám z toho vznikne zase Poissonova rovnice (možná tam má být někde opačné znaménko),
A pokud na obě strany rovnice aplikujeme operátor rotace, dostaneme vlastně tu rovnici, co už jsem napsal dříve.
Později ti ukáži, kam se ten posuvný proud ztratil, ale až poté, co tě přejde chuť rozporovat samotné rovnice pro čtyřpotenciál.
Offline
#45 12. 02. 2019 09:04
Re: Magnetické pole generované dodatečným proudem
↑ MichalAld:
Sice se sám sobě divím, že do tohoto podivného vlákna ještě píšu, protože sledovat, jakou že situaci tu právě řešíte a skoky z třívektorového do čtyřvektorového popisu nestíhám, ani nechápu jejich smysl. Komentuji tedy především poslední příspěvek.
Za podmínek o kterých mluvíme, tj 2. derivace podle času je nulová, nám z toho vznikne zase Poissonova rovnice
Pokud vím, bude také platit:
a tedy
Píšeš, že 2. derivace A podle času má být v uvažované situaci (ať už je to aktuálně jakákoli) nulová. To ale znamená, že musí být nulová i časová derivace E (případ  rozebírat nebudu, ale zdá se mi, že minimálně při konstantním proudu nemůže nastat, pokud nemá být porušena rovnice kontinuity).
rozebírat nebudu, ale zdá se mi, že minimálně při konstantním proudu nemůže nastat, pokud nemá být porušena rovnice kontinuity).
A protože posuvný proud je definován jako  , je prostě "za podmínek, o kterých mluvíme" nulový a tedy ho je možné ze všech rovnic vyškrtat a pak se mu posmívat, že nemá žádný vliv. Ale co je na tom tak objevného, to nevím. Nebo mi zas něco uniká?
, je prostě "za podmínek, o kterých mluvíme" nulový a tedy ho je možné ze všech rovnic vyškrtat a pak se mu posmívat, že nemá žádný vliv. Ale co je na tom tak objevného, to nevím. Nebo mi zas něco uniká?
Offline
#46 12. 02. 2019 09:20 — Editoval MichalAld (12. 02. 2019 09:25)
Re: Magnetické pole generované dodatečným proudem
LukasM napsal(a):
Píšeš, že 2. derivace A podle času má být v uvažované situaci (ať už je to aktuálně jakákoli) nulová. To ale znamená, že musí být nulová i časová derivace E (případ
rozebírat nebudu, ale zdá se mi, že minimálně při konstantním proudu nemůže nastat, pokud nemá být porušena rovnice kontinuity).
Jenže to je zrovna ta situace kterou řešíme - tudíž zrovna na tohle se musíme zaměřit.
Jde přesně o tuhle situaci - konstantní proud, tedy konstantní (v čase) A, a změna E pochází jen ze změny 
A rovnice kontinuity - ta je splněna určitě, protože čytřdivergence el. mag. potenciálu je vždy nulová, díky ... (díky Lorenzově kalibrační podmínce, ale o tom jsem chtěl mluvit až později...protože to je přesně to, kam se "schoval" ten posuvný proud, alespoň mi to tak přijde)
PS: Já netvrdím, že mám pravdu....(aspoň ohledně posuvného proudu)....
Offline
#47 13. 02. 2019 09:34 — Editoval KennyMcCormick (13. 02. 2019 10:07)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Magnetické pole generované dodatečným proudem
Jak to víš ?
Zkus si to.
Každopádně je odvodím z tohoto:
Ani tyhle rovnice nejsou tvým řešením splněny.
Napadl mě obecný důkaz příspěvku posuvného proudu k poli: Protože hustota posuvného proudu přispívá k rotaci 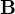 v nejméně jednom bodu prostoru, přispívá i k magnetickému poli, což mělo být dokázáno.
v nejméně jednom bodu prostoru, přispívá i k magnetickému poli, což mělo být dokázáno.
↑ LukasM:
Konstantní proud končí na desce kondenzátoru, mezi deskami pokračuje konstantní posuvný proud, na druhé desce posuvný proud končí a zase začíná konstantní vodivý proud, takže rovnice kontinuity platí.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#48 13. 02. 2019 23:30
Re: Magnetické pole generované dodatečným proudem
KennyMcCormick napsal(a):
Každopádně je odvodím z tohoto:
Ani tyhle rovnice nejsou tvým řešením splněny.
O jakém "mém řešení" to vlatně mluvíš? Já žádné "řešení" nikde nezmiňoval, pokud vím...
Máme funkci proudové hustoty, konstantní v čase, 
Z toho dokážeme (s využitím rovnice kontinuity) určit i funkci nábojové hustoty, která bude tvaru (možná s opačným znaménkem)
Takže máme pole konstantní proudové hustoty a lineárně rostoucí nábojové hustoty, obojí známe.
Připouštím, že je to pořád idealizovaná představa, ale zatím si s tím asi vystačíme.
To ale není žádné "řešení", to je prostě popis té situace, kterou máme.
Řešením je nalézt skalární potenicál  a vektorový potenciál
a vektorový potenciál  . Ten první vlastně ani hledat nemusíme, protože elektrické pole nás nezajímá. Takže stačí najít A.
. Ten první vlastně ani hledat nemusíme, protože elektrické pole nás nezajímá. Takže stačí najít A.
A když to uděláme (což není až takový problém, protože d'Alembertova rovnice nám pro konstantní pravou stranu přejde na tu Laplaceovu - a tam už řešení známe (je to ekvivalent Coulombova zákona).
No a B = rot A. Když A nezávisí na nějakém "posuvném proudu", nebude ani B. Navíc můžeme na rovnici ten operátor aplikovat rovnou, a dostaneme to, co už jsem napsal několikrát předtím, tedy


Podle mě tady není co k diskusi, jediné co můžeš rozporovat je obecná platnost těch výchozích rovnic. A s tím problém nemám - můžu ti ukázat, že jsou s Maxwellkami ekvivalentní.
Offline
#49 13. 02. 2019 23:38
Re: Magnetické pole generované dodatečným proudem
Ještě poznámka - z rovnice rot B = něco nelze B určit, ani při vhodných okrajových podmínkách né. Existuje nekonečné množství polí, které může tuhle rovnici splňovat. Takže stavět na tomhle nějaký důkaz je trochu problematické. A problematická je tedy i diskuse o tom, co vlastně v konkrétním bodě pole B vytvořilo.
Zatímco z rovnice  pole A určíme - a stačí nám okrajová podmínka že v nekonečné vzdálenosti bude nulové. Dokonce to jde napsat i analyticky - a příspěvky k A v každém bodě pochází od všech bodů, kde je ta pravá strana nenulová. A v tomto smyslu můžeme tedy mluvit o tom, co pole A (v daném bodě) vytvořilo. Ale je to samozřejmě pořád to "v tomto smyslu".
pole A určíme - a stačí nám okrajová podmínka že v nekonečné vzdálenosti bude nulové. Dokonce to jde napsat i analyticky - a příspěvky k A v každém bodě pochází od všech bodů, kde je ta pravá strana nenulová. A v tomto smyslu můžeme tedy mluvit o tom, co pole A (v daném bodě) vytvořilo. Ale je to samozřejmě pořád to "v tomto smyslu".
Offline
#50 13. 02. 2019 23:53 — Editoval MichalAld (14. 02. 2019 00:00)
Re: Magnetické pole generované dodatečným proudem
KennyMcCormick napsal(a):
Proto nemůžeš použít rovnici
, do které dosadíš
, abys získal magnetické pole vygenerované posuvným proudem, pokud posuvný proud sám o sobě nesplňuje Maxwellovy rovnice.
Tohle celkem dává smysl ... já to totiž myslím přesně naopak.
Nechci do Maxwellek dosazovat jen posuvný proud, abych získal magnetické pole vytvořené jen posuvným proudem.
Chci do Maxwellek dosazovat jen normální proud - a získat jak magnetické pole, které tento proud vytvoří, tak elektrické pole, které tento proud vytvoří (a z nějž můžu určit ten posuvný proud).
A v podstatě otázka zní, jestli to dokážu udělat tak, abych se o elektrické pole nemusel vůbec starat. Jestli dokáži najít vztah, který mi ze zadaného (normálního) proudu spočítá magnetické pole. Což podle mě není problém (a už jsem to tady asi 5x napsal, v různých variantách).
A to je celé, o co mi vlastně jde. Známe normální proud, a to nám stačí, abychom dokázali (kompletně) určit magnetické pole. Že se tam u toho objeví ještě i nějaký posuvný proud či el. pole nás nemusí vůbec zajímat. Že ten posuvný proud je takový vedlejší důsledek toho, jak jsme situaci narafičili, a pro určení magnetického pole jej vůbec znát nepotřebujeme.
Je to vlastně to samé, jako bychom onu Maxwellku nepsali v běžně uváděném tvaru, ale psali bychom ji jako (vynechávám všechny konstanty):
A interpretovali ji tak, že (obyčejný) proud je zdrojem jak B, tak i posuvného proudu, dle detailů situace.
Pokud na ni aplikujeme operátor divergence, dostaneme, jak proud tvoří posuvný proud, pokud na ni aplikujeme operátor rotace, dostaneme jak proud tvoří magnetické pole.
Ale samozřejmě - tahle interpretace platí jen pro konstatní j - tedy konstantní (v čase) dE/dt, a hlavně tedy konstantní (v čase) B.
Offline
- Hlavní strana
- » Fyzika
- » Magnetické pole generované dodatečným proudem (TOTO TÉMA JE VYŘEŠENÉ)


 . Nemůžeš. Ty totiž nevíš, zda ta rovnice platí ve všech situacích, protože k tomu, abys ji odvodil, jsi předpokládal platnost Maxwellových rovnic. Jinými slovy: Pokud Maxwellovy rovnice vrátí s jistotou správnou odpověď na daný vstup, pak tvoje rovnice správnou odpověď vrátí taky. Jenomže pokud vstup nesplňuje Maxwellovy rovnice, pak nevíš, zda Maxwellovy rovnice na daný vstup vrátí správnou odpověď, a tak nevíš, zda správnou odpověď vrátí tvá rovnice. Možná ano.
. Nemůžeš. Ty totiž nevíš, zda ta rovnice platí ve všech situacích, protože k tomu, abys ji odvodil, jsi předpokládal platnost Maxwellových rovnic. Jinými slovy: Pokud Maxwellovy rovnice vrátí s jistotou správnou odpověď na daný vstup, pak tvoje rovnice správnou odpověď vrátí taky. Jenomže pokud vstup nesplňuje Maxwellovy rovnice, pak nevíš, zda Maxwellovy rovnice na daný vstup vrátí správnou odpověď, a tak nevíš, zda správnou odpověď vrátí tvá rovnice. Možná ano. a
a  (a už žádné jiné), celkové pole bude
(a už žádné jiné), celkové pole bude  .
.