Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#5 29. 01. 2019 18:48 Příspěvek uživatele Flaky byl skryt uživatelem Flaky.
#7 29. 01. 2019 19:21 — Editoval jardofpr (30. 01. 2019 11:09)
Re: Borelovská mn.
Flaky napsal(a):
Na interval
se zobrazí všechny body
takové, že
takto napísané mi veľmi nedáva zmysel ako to myslíš
tá množina pre neklesajúcu funkciu môže naberať len 4 tvary čo je jednoduché si rozmyslieť
každý z nich je borelovskou množinou a máš prakticky hotovo
otvorený interval nie je potom problém napísať pomocou množín typu ![kopírovat do textarea $(-\infty,y]$](/mathtex/ab/ab9b16cf8760d45ffacc99395182d3b2.gif)
EDIT: asi myslíš ![kopírovat do textarea $f^{-1}((-\infty,y]) = \{b\,\in\mathbb{R}\,:\,f(b)\leq y\} $](/mathtex/32/32b7cc267a002cd21bbb46adaf4ece0f.gif) len si to zvláštne popísal/zapísal
len si to zvláštne popísal/zapísal
Offline
#10 21. 02. 2019 11:37
Re: Borelovská mn.
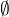 to pokud má funkce hodnoty mimo pás
to pokud má funkce hodnoty mimo pás ![kopírovat do textarea $(-\infty , y]$](/mathtex/e0/e0b09783cf4aa09daead7655a31f0f65.gif) a žádné takové
a žádné takové  , pro které by
, pro které by 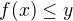 neexistuje
neexistuje
nebo to můžou být 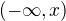 či
či ![kopírovat do textarea $(-\infty ,x]$](/mathtex/bf/bfa728a26faca8ec18056f27bb22378d.gif) , kde x je nejvetší takové, že
, kde x je nejvetší takové, že 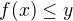
nebo může funkce celá ležet v pásu a mít def. obor R
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
#11 21. 02. 2019 12:54 — Editoval jardofpr (21. 02. 2019 12:55)
Re: Borelovská mn.
↑ Flaky:
áno, vďaka neklesajúcosti sa toto ľahko vyvodí
podobne sa dá spracovať vzor množiny typu 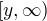 , čo si určite ľahko rozmyslíš
, čo si určite ľahko rozmyslíš
t.j. vzory takýchto množín sú borelovské množiny pri neklesajúcej funkcii
vieme napísať otvorený interval pomocou množín uvedeného typu?
pozn. pre ďalší krok: pre funkcie platí ![kopírovat do textarea $f^{-1}[A\cap B] = f^{-1}[A]\cap f^{-1}[ B]$](/mathtex/a1/a1e2e5ec5a72b74551df4ffd406c19e4.gif) a
a ![kopírovat do textarea $f^{-1}[A\cup B] = f^{-1}[A]\cup f^{-1}[ B]$](/mathtex/e2/e29b863b9cabe739693d6d12840885a8.gif)
+ borelovské množiny v  tvoria
tvoria 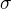 -algebru
-algebru
Offline
#14 21. 02. 2019 14:30 — Editoval Flaky (21. 02. 2019 14:42)
Re: Borelovská mn.
↑ jardofpr: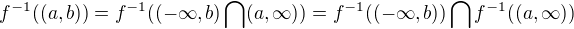 ,
,
akorat bych tam potřeboval dostat polouzavrene intervaly
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline

![kopírovat do textarea $f^{-1}((-\infty,y])$](/mathtex/17/17a22e4b594cb1880dcb25aea1e8afb4.gif) pre monotónnu funkciu?
pre monotónnu funkciu? neklesajúca .. ako môže tá množina vyzerať?
neklesajúca .. ako môže tá množina vyzerať?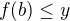
![kopírovat do textarea $\emptyset, (-\infty,x), (-\infty,x]$](/mathtex/86/86fe0407778e722408ecc917822481a7.gif) alebo
alebo 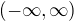
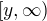 za pomoci průniku a sjednocení.
za pomoci průniku a sjednocení.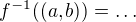
![kopírovat do textarea $(a,b)=(-\infty,a]^C\cap [b,\infty)^C$](/mathtex/ce/ced0e59b67b02ee38054c9c0c5180818.gif)
![kopírovat do textarea $f^{-1}[A^C] = (f^{-1}[A])^C$](/mathtex/ed/ede3a7634e41c615ea1458bb3a32fe36.gif)
![kopírovat do textarea $f^{-1}(a,b)=f^{-1}((-\infty ,a]^{C}\bigcap_{}^{}[b,\infty )^{C})^{}=f^{-1}((-\infty ,a]^{C})\bigcap_{}^{}f^{-1}([b,\infty )^{C})=[f^{-1}((-\infty ,a])]^{C}\bigcap_{}^{}[f^{-1}([b,\infty ))]^{C}$](/mathtex/82/82358bc92599cb66bf62bff93bbef458.gif) , a tedy vnitřky závorek jsou borelovské množiny, tedy i jejich doplňky a poté i jejich průnik z vlastností
, a tedy vnitřky závorek jsou borelovské množiny, tedy i jejich doplňky a poté i jejich průnik z vlastností  algebry.
algebry.