Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 03. 2019 09:25
- stuart clark

- Příspěvky: 1015
- Reputace: 7
function
Let  is defined for
is defined for  and has a continuous derivatives. If
and has a continuous derivatives. If  satisfies
satisfies  and
and  Then maximum value of
Then maximum value of  is
is
and also proving  has minima and function
has minima and function  is concave upwards
is concave upwards
Offline
#2 17. 03. 2019 12:50
#5 17. 03. 2019 16:45
Re: function
hey guys,
to follow the comment from ↑ Bati:,
I would add that I believe that also proving global uniqueness for solution on interval 
is necessary to give the numerical solution some weight, assuming some numerical method for ODE was used
in case of ODE with more solutions, numerical approximation of one of the solutions
can be not anywhere close to full picture
(convexity and minimum of the function is very easy in this problem,
I'm just getting curious about the requested maximum estimate)
Offline
#6 17. 03. 2019 18:29
Re: function
↑ laszky:
So you basically say that your result is as reliable as a weather forecast... and yes, a bad forecast is pretty useless
↑ jardofpr:
Good point
Offline
#7 23. 03. 2019 13:18
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: function
↑ jardofpr:
How can i find convexity and minimum of function. Thanks
Offline
#8 23. 03. 2019 17:03
Re: function
hi ↑ stuart clark:
There is 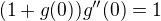 therefore
therefore 
together with  it says that the function has at least local minimum in
it says that the function has at least local minimum in  .
.
Furthermore 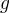 is defined for
is defined for  so there is
so there is  on the domain of the function
on the domain of the function
(note that inequality is sharp, never equality)
so in each  expressions
expressions  and
and 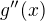 are either both strictly positive or both strictly negative.
are either both strictly positive or both strictly negative.
As  and given
and given 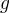 and its derivatives are continuous,
and its derivatives are continuous, 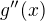 stays always positive
stays always positive
and therefore 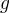 is concave upwards = convex.
is concave upwards = convex.
This fact also says that  is strictly increasing, and together with
is strictly increasing, and together with  this gives
this gives and
and  , which makes the minimum in
, which makes the minimum in  global.
global.
To the last unanswered question I was yet able to find out that  by analytical approach
by analytical approach
but this is for sure not maximum as it cannot be reached.
Offline
