Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Obsah oblasti ohraničené křivkami (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 04. 2019 15:52
Obsah oblasti ohraničené křivkami
Dobrý den, mám tu jeden příklad co se týče obsahu oblasti ohraničené křivkami, moc si s těmihle typy úloh nevím rady, tak kdyby mi někdo dokázal pomoct, byl bych jen rád.
Křivky: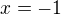
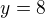

Náčrtek bych nejspíš zvládl, ale ty průsečíky, podle kterých počítat integrál, u těch si nejsem moc jistej.
počítal bych tak, že bych za a
a  dosadil do té poslední rovnice, ale teď nevím právě, nejprve asi postupně, jednou za x, jednou za y?
dosadil do té poslední rovnice, ale teď nevím právě, nejprve asi postupně, jednou za x, jednou za y? 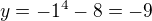
a teď bych dosadil za ypsilon: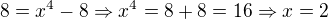
Takže bych měl meze od -9 po 2? Ale tak to vlastně nejde, to -9 je průsečík na y.
Offline
- (téma jako vyřešené označil(a) NeuRotiCk)
#3 01. 04. 2019 16:46
Re: Obsah oblasti ohraničené křivkami
Nakreslil jsem si obrázek, snad dobře.
Oblast S1 by byl teda integrál v mezích od -1,8 po -1? Akorát jak se došlo na -1,8? To mi ukázal wolfram.
A potom jaká funkce by byla v integrálu? Pokud platí, že obsah = horní fce - dolní. Horní by v tomhle případě bylo to 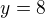 a dolní
a dolní ?
?
Nebo tam furt dělám nějakou chybu?
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Obsah oblasti ohraničené křivkami (TOTO TÉMA JE VYŘEŠENÉ)
