Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » vázané extrémy - stacionární body (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 05. 2019 13:32
vázané extrémy - stacionární body
Dobrý den, mám funkci 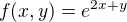 s vazbou
s vazbou 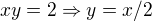
Nepoužíval jsem metodu multiplikátorů, ale tu druhou, takže mi vznikla funkce h(x)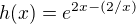
Derivací téhle funkce jsem dostal: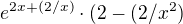
Ale teď si nevím rady, jak určit stacionární body, nic mě nenapadá, s takovýmhle typem příkladu jsem se setkal poprvé.
Kdyby mi někdo dokázal poradit byl bych mu vděčný.
Předem děkuji za jakoukoliv odpověď.
Offline
- (téma jako vyřešené označil(a) byk7)
#2 20. 05. 2019 13:36 — Editoval vlado_bb (20. 05. 2019 13:37)
Re: vázané extrémy - stacionární body
↑ NeuRotiCk: Kedy je sucin dvoch cisel nulovy? Dalej, naozaj z 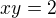 vyplyva
vyplyva 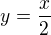 ?
?
Offline
#4 20. 05. 2019 13:58
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » vázané extrémy - stacionární body (TOTO TÉMA JE VYŘEŠENÉ)

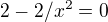 ?
?