Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál s odmocninou (TOTO TÉMA JE VYŘEŠENÉ)
#2 20. 05. 2019 19:22 Příspěvek uživatele Al1 byl skryt uživatelem Al1.
#3 20. 05. 2019 21:50
Re: Integrál s odmocninou
↑ Johana16:
Zdravím,
zkusil jsem substituci ![kopírovat do textarea $1+\sqrt[]{x^{2}+2x+2}=x+t+1$](/mathtex/f6/f6349431d6402e671d5bd1fa8ffa3091.gif) . Nedává úplně složité výpočty.
. Nedává úplně složité výpočty.
Zkušenější kolegové poradí třeba snazší postup.
Offline
#4 20. 05. 2019 22:59
Re: Integrál s odmocninou
↑ Al1:
Dobrý den, také jsem to zkoušela. Akorát jsem tam nedávala na obě strany ty 1. Výpočet pak nebyl těžký, jen nevim, zda to lze takto počítat. Zda se zde může použít Eulerova substituce :-(
Takže myslíte, že by to mohl být správný postup?
Děkuji
Offline
#5 20. 05. 2019 23:08
Re: Integrál s odmocninou
↑ Johana16:
Ano, Eulerova substituce je vhodná metoda. A vyjde to nastejno, když zavedeš substituci ![kopírovat do textarea $\sqrt[]{x^{2}+2x+2}=x+t$](/mathtex/53/537dfd2c3a0b80cc2a8ddd671f06f53e.gif) , protože při mém postupu se stejně hned 1 od obou stran odečte. :-)
, protože při mém postupu se stejně hned 1 od obou stran odečte. :-)
Offline
#6 20. 05. 2019 23:31
Re: Integrál s odmocninou
Pozdravujem ↑ Al1:,
Mozno by sme mohli najprv sa zbavit odmicniny v menovateli.
( no zatial som nic s tym nerobil)
Dobru noc
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 21. 05. 2019 00:04 Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš.
#10 21. 05. 2019 11:10
#11 21. 05. 2019 14:59
Re: Integrál s odmocninou
↑ vlado_bb:
Jo vlastně. Pro žádné.
Ale tak kdyby byl příklad jako tento?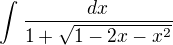
Děkuji
Offline
#12 21. 05. 2019 15:09
#13 21. 05. 2019 16:17
Re: Integrál s odmocninou
↑ vlado_bb:
pokud bych udělala substituci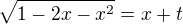
a poté umocnila, tak jak z výrazu 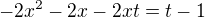 získám vyjádřené
získám vyjádřené  ?
?
Děkuji moc za pomoc!
Offline
#14 21. 05. 2019 16:18
#15 21. 05. 2019 17:40 — Editoval Al1 (21. 05. 2019 17:41)
Re: Integrál s odmocninou
↑ Johana16:
Pokud existuje rozklad na součin výrazu 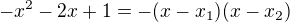 ( a to existuje), pak se volí Eulerova substituce
( a to existuje), pak se volí Eulerova substituce 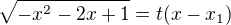 nebo
nebo 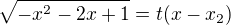
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál s odmocninou (TOTO TÉMA JE VYŘEŠENÉ)
![kopírovat do textarea $\int_{}^{}\frac{dx}{1+\sqrt[]{x^{2}+2x+2}}$](/mathtex/3e/3e5e6b44ae68d7da05e0bfa214c7111b.gif)

 ?
?  existuje tento vyraz?
existuje tento vyraz?