Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 … 13 14 15 16 17 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton
#351 05. 05. 2019 09:23 — Editoval krakonoš (05. 05. 2019 09:26)
Re: Limitny maraton
↑↑ vanok:
Problem(74)
Ahoj.
V tomto případě stačí použít L'Hospitalovo pravidlo, případně postup pro výpočet limity ,označme ji L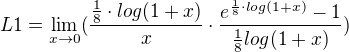
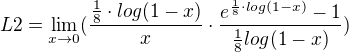

Při výpočtu 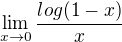 lze použít porovnání logaritmu vůči x s inverzní funkcí logaritmu vůči x t.j.
lze použít porovnání logaritmu vůči x s inverzní funkcí logaritmu vůči x t.j.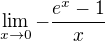
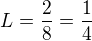
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#352 05. 05. 2019 09:48 — Editoval stuart clark (05. 05. 2019 09:58)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
Thanks Vanok.
For 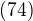 Using
Using 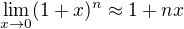
So 
Problem 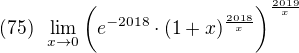
Offline
#353 05. 05. 2019 10:42
Re: Limitny maraton
↑ stuart clark:
Problem (75)
Hi Stuart Clark
 ( from Taylor function log())
( from Taylor function log())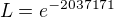
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#354 05. 05. 2019 11:00
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
Thanks ↑ krakonoš:
Problem 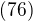 If
If 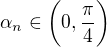 is the root of the equation
is the root of the equation 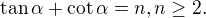
Then value of 
Offline
#355 05. 05. 2019 19:49 — Editoval krakonoš (05. 05. 2019 20:22)
Re: Limitny maraton
↑ stuart clark:
Hi Stuart Clark
Problem(76)
That's just my fast=paced assault.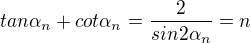

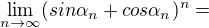

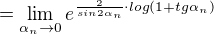

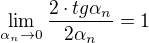

tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#356 06. 05. 2019 08:34 — Editoval stuart clark (08. 05. 2019 13:38)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
Thanks ↑ krakonoš:
My solution is almost same except last  lines
lines
From 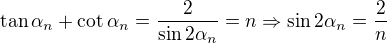
And 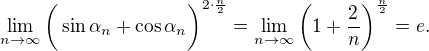
Problem 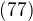 Finding
Finding 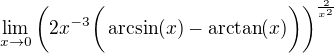
without using series expansion and D L Hopital Rule
Offline
#357 06. 05. 2019 12:33 — Editoval krakonoš (07. 05. 2019 15:59)
Re: Limitny maraton
↑ stuart clark:
Problem( 77)
Hi Stuart Clark
Internal function limit is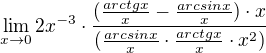
I think,It's the similar situation as 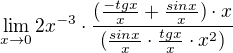
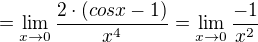
I am afraid that the given limit won't exist.
There is the same problem (it is negative).
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#358 08. 05. 2019 12:25 — Editoval stuart clark (08. 05. 2019 12:29)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
Thnaks ↑ krakonoš: may be you have missed something
By series expansion of the arcsine and arctangent,
So we get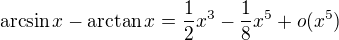
So we have ![kopírovat do textarea $ \lim_{x\to 0} [1-\tfrac14x^2+o(x^2)]^{2/x^2} = \lim_{x\to 0} e^{\left(\frac{2}{x^2}\log(1-\tfrac14x^2+o(x^2))\right)}$](/mathtex/2c/2cbbe36ddb20aa1208c23ea20c772af1.gif)
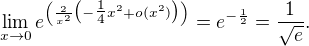
But i am unable to solve it without series exp.
Offline
#359 08. 05. 2019 13:32 — Editoval krakonoš (08. 05. 2019 13:36)
Re: Limitny maraton
↑ stuart clark:
H Stuart Clark
There is not function arcsinx-arctgx.In the problem (77) is function .
.
I assumed 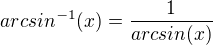
tgx>x>sinx
arctg<x<arcsinx
1/arctgx>1/arcsinx for x>0
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#360 08. 05. 2019 13:38 — Editoval stuart clark (08. 05. 2019 13:39)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
Ohoo my bad you are right ↑ krakonoš:.
Can you solve it for original problem.(I have edited it). Thanks
Offline
#361 19. 05. 2019 12:45
Re: Limitny maraton
Problem (78).
Dalsi (jednoduchy?) problem.
Najdite  .
.
(Dokazete to bez L’Hôpital-oveho pravidla?)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#362 20. 05. 2019 19:40
#364 21. 05. 2019 20:55
Re: Limitny maraton
↑ krakonoš:↑ vanusok:
Pozdravujem,
Ano toto cvicenie ma ozaj vela moznych rieseni.
No dal som ho sem, aby ste sa trochu zabavili.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#365 21. 05. 2019 21:08
Re: Limitny maraton
Problem(79).
Nech 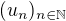 je ohranicena postupnost, taka ze
je ohranicena postupnost, taka ze 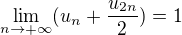 .
.
Co mozete povedat o postupnosti 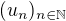 ?
?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#366 21. 05. 2019 22:50 — Editoval krakonoš (21. 05. 2019 22:51)
Re: Limitny maraton
↑ vanok:
Problem(79)
Ahoj.
Posloupnost je shora i zdola omezená. Obecně to samo o sobě nestačí k existenci limity, protože například vybraná podposloupnost sudých členů může mít jinou limitu než podposloupnost lichých členů. To by ovšem neexistovala ani zadaná limita, která je rovna jedné.
Posloupnost má tedy konečnou limitu L ,vybrané podposloupnosti rovněž.
L plus L/2 je rovno 1.
Limita posloupnosti un by tedy měla být rovna 2/3.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#367 22. 05. 2019 06:33
Re: Limitny maraton
Cau ↑ krakonoš:,
Najprv skutocne dana postupnost konverguje k 2/3.
Poznamename najprv, ze ak postupnost un konverguje k L tak vdaka predpokladu sa 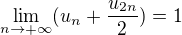 , mame L+L/2=1, co da, ze L=2/3.
, mame L+L/2=1, co da, ze L=2/3.
No vsak, treba dokazat, ze un konverguje.
V tvojom pokusy dokazu predpokladas, ze konvergenciu vybranych postupnosti parnych a neparnych clenov. No o tom « à priori » nemozes este nic povedat.
No vsak je mozne dokazat konvergenciu postupnosti (un) sporom.
Tak predpokladajme, ze (un) nekonverguje.
No vsak akoze je ohranicena, tak existuje vybrana postupnost 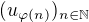 ktora konverguje k
ktora konverguje k 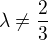
A potom som pokracoval podobne uvahy ako ty. (No iste to kazdy dokaze urobit, alebo mam pokracovat tie moje?).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#368 22. 05. 2019 09:02 — Editoval krakonoš (22. 05. 2019 09:20)
Re: Limitny maraton
↑ vanok:
Ahoj.
Z každé omezené posloupnosti lze vybrat konvergentní podposloupnost, jejíž limita je vlastně hromadný bod posloupnosti.
Kdyby posloupnost un měla aspoň dva hromadné různé body, pak by A)
i posloupnost u2n měla buď rovněž dva různé hromadné body a nekonvergovala by také, takže i posloupnost( un plus u2n/2).
Aspoň já si představuji, že pokud dvě limity neexistují, může existovat limita jejich rozdílu pouze v případě rovnosti členů ( mám na mysli např lim(1/x-1/x) pro x jdouci k nule), to však v tomto případě nenastává.
Nebo B) un ma aspoň dva různé hromadné body, u2n konverguje, pak by ale existovaly vybrané podposloupnosti. z posloupnosti (un plus u2n/2),které mají různé hromadné body,a nemohla by zadaná limita, ktera má být rovna jedné vůbec existovat.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#369 22. 05. 2019 09:54
Re: Limitny maraton
↑ krakonoš:,
Ano to je klucova myslienka.
👍
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#370 25. 05. 2019 10:13
#371 25. 05. 2019 15:18 — Editoval vanok (25. 05. 2019 15:19)
Re: Limitny maraton
Ahoj ↑ krakonoš:,
Ja som uz pocital 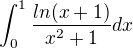 , ktory je
, ktory je  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#372 25. 05. 2019 17:25 — Editoval krakonoš (25. 05. 2019 21:10)
Re: Limitny maraton
↑ vanok:
Ahoj.
Tady jsou ale jine meze.Tento priklad (a jeste dalsi dva) jsem nasla ve foru pro VŠ -uvod do studia cca cerven 2018.Jeden je tam spocten,dalsi dva ne.Tak jsem si vsechny spocetla sama a zajimalo me,jaky postup zvoli ostatni.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#373 25. 05. 2019 21:12
#374 26. 05. 2019 11:46
#375 29. 05. 2019 15:48 — Editoval krakonoš (29. 05. 2019 17:20)
Re: Limitny maraton
↑ stuart clark:
Problem (81)
Hi Stuart clark.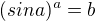

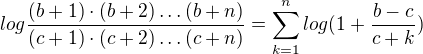
For 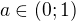 is
is 
For  is
is 
For a>0, where sin a<0 the Expression  is not defined for some
is not defined for some 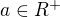 .For other a is
.For other a is 
For b<c is 
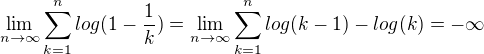
The function  is not growing, continuity for x>1, not negative
is not growing, continuity for x>1, not negative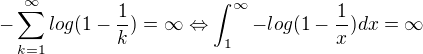 (The integral criterion)
(The integral criterion)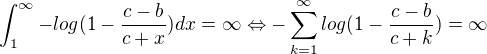
The limit
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
Stránky: 1 … 13 14 15 16 17 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton

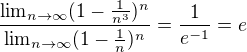

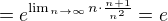
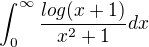
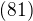
 . Then
. Then 