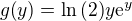Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 05. 2019 10:13 — Editoval NeuRotiCk (30. 05. 2019 10:15)
Vázané extrémy
Dobrý den, na zkoušce jsem měl příklad na vázané extrémy, kde se mi sice podařilo najít stacionární bod x, ale ten neodpovídal def. oboru, tak nevím jestli sem neudělal někde chybu, kdyby mi to někdo mohl zkontrolovat:
příklad: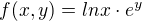 při vazbě
při vazbě 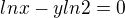
Já sem si z vazby vyjádřil y, protože podle mě jde jednoznačně vyjádřit a nemusím počítat přes multiplikátory: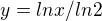
Pak jsem teda zavedl novou funkci: 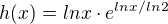
první derivací dostanu: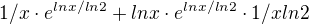
z té derivace sem vytkl do tvaru: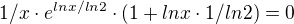
celou rovnici se podělil tím 1/x a vyšlo mě: 
a to se rovná: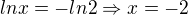
Ale přece -2 nepatří do Definičního oboru logaritmu ne? Nebo dělám někde chybu, kterou nevidím?
Předem děkuji za jakoukoliv odpověď.
Leda teda to spočítat znova přes multiplikátory a tady ten způsob tady na tomhle příkladu asi selhává.
Přes multiplikátory vyšly SB: ![kopírovat do textarea $[1/2,-1,-1/e]$](/mathtex/83/83d39ccdd46f964a0244495c8f65a35a.gif)
Offline
- (téma jako vyřešené označil(a) NeuRotiCk)
#2 30. 05. 2019 10:31
Re: Vázané extrémy
Offline
#5 30. 05. 2019 17:00 — Editoval NeuRotiCk (30. 05. 2019 17:02)
Re: Vázané extrémy
Takhle by to šlo taky, ale mě vždycky trvá než dojdu na to, jak upravit ten logaritmus, takhle mě logaritmus pěkně vypadl, ale děkuju za nápad.
Ale jo, už to vidím, bylo by to teda jednodušší, já si nebyl jistej jak tam pracovat s těma logaritmama, ale tam se všechno vykrátí, takle je to asi jednodušší no. Děkuju.
EDIT: ale stejně, ten kořen 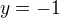 musím dosadit přece do té vazby, abych spočítal
musím dosadit přece do té vazby, abych spočítal  .
.
A to zpaměti nedám nebo někde dělám chybu.
Offline
#6 30. 05. 2019 19:54
Offline

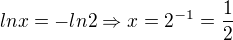
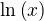 ?
?