Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lokální extrémy funkce dvou proměnných (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 06. 2019 15:04
Lokální extrémy funkce dvou proměnných
Dobrý den, mám jeden příklad, se kterým si nevím moc rady, pořád mě to jaksi nevychází.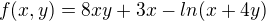
první derivace:
podle x: 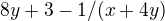
podle y: 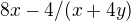
Stacionárni body sem vyřešil tak, že jsem obě rovnice vynásobil tím zlomkem a pak sem je sečetl:
rovnice:
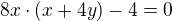
po roznásobení sem dostal rovnice:
1. 
2. 
první rovnici sem vydělil y a druhou x a dostal sem rovnice ve tvaru:
1. 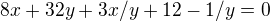
2. 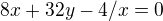
první rovnici sem vynásobil  a přičetl ke druhé:
a přičetl ke druhé: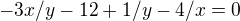
No a ted nevím jak zjistit ty body, různě sem zkoušel, převedl sem rovnici do tvaru: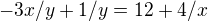 z té levé strany sem vytkl 1/y a dostal sem:
z té levé strany sem vytkl 1/y a dostal sem: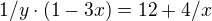 tu celou rovnici sem vynásobil
tu celou rovnici sem vynásobil  a pak sem vytkl
a pak sem vytkl  na levé a na pravé straně sem vytkl
na levé a na pravé straně sem vytkl 
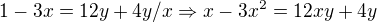

takže body pro  by mě vyšly
by mě vyšly ![kopírovat do textarea $[0,\pm 1/3]$](/mathtex/cc/cc691e0e8ed6059b586403bf444f9673.gif) a
a  .
.
Ale zdá se mi to příliš zdlouhavé a taky se mi to nezdá příliš správně.
Kdyby někdo věděl, jak to zjednodušit nebo mi poradit kde dělám chybu byl bych mu vděčný, předem děkuji.
Offline
- (téma jako vyřešené označil(a) NeuRotiCk)
#2 10. 06. 2019 15:20
Re: Lokální extrémy funkce dvou proměnných
↑ NeuRotiCk:
Ahoj, zkusil bych na zacatku od druhe rovnice odecist ctyrnasobek prvni rovnice.
Offline
#6 10. 06. 2019 15:41
Re: Lokální extrémy funkce dvou proměnných
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lokální extrémy funkce dvou proměnných (TOTO TÉMA JE VYŘEŠENÉ)

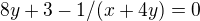
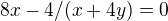
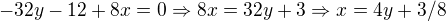 takhle? To zní rozumněji, dosadil bych za x do druhé rovnice a dopočítal
takhle? To zní rozumněji, dosadil bych za x do druhé rovnice a dopočítal