Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 … 14 15 16 17 18 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton
#376 30. 05. 2019 11:03
#377 30. 05. 2019 16:05
Re: Limitny maraton
↑ vanusok:
Ahoj.
Díky moc.
Měla jsem spočítat 3 příklady.Ty ostatní byly v pohodě,tenhle mi připadal nejprve nejlehčí,ale opak byl pravdou.Ještě jsem se s tímto typem v literatuře nesetkala.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#378 30. 05. 2019 22:53
Re: Limitny maraton
Ahoj ↑↑ krakonoš:
Problem 80.
Len mala poznamka .
Podla wa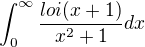
je  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#379 30. 05. 2019 23:41 — Editoval krakonoš (31. 05. 2019 10:25)
Re: Limitny maraton
↑ vanok:
Ahoj.
Wa je pocitacovy program?.Uz vidim pocetni chybu!Je tam spatne spoctena derivace.
Takze asi mas pravdu.Diky
Po pravde receno,nevidim zatim funkci,ze ktere by integral konvergoval &podil funkci dal vlastni limitu.A k logaritmu primitivni funkci,kteta by byla omezena,neurcim.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#380 31. 05. 2019 02:42
Re: Limitny maraton
↑ krakonoš: Wa :)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#381 31. 05. 2019 12:18 — Editoval krakonoš (01. 06. 2019 13:44)
Re: Limitny maraton
↑ vanok:
Ahoj
Možná by šlo uvažovat o funkci  ,
,
(to by už vlastní limitu při podílu funkcí dávalo) a integrál  by měl konvergovat vzhledem ke konvergenci odpovídající číselné řady .Pripadne dokazat konvergenci rady log(n plus 1)/nnadruhou s pomoci Eulerovy konstanty.
by měl konvergovat vzhledem ke konvergenci odpovídající číselné řady .Pripadne dokazat konvergenci rady log(n plus 1)/nnadruhou s pomoci Eulerovy konstanty.
Jinak mě už nic nenapadá.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#382 09. 06. 2019 20:45 — Editoval vanok (09. 06. 2019 21:36)
Re: Limitny maraton
KProblem (82)
Polozme 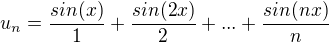 .
.
Dokazte, ze tato postupnost konverguje v  ;
; 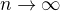 k nenulovej limite.
k nenulovej limite.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#383 10. 06. 2019 09:07
#384 10. 06. 2019 10:42
Re: Limitny maraton
Cau ↑ krakonoš:,
Mozno aj to je mozna cesta k rieseniu.
No je aj o mnoho prirodzenejsie riesenie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#386 10. 06. 2019 14:54 — Editoval krakonoš (10. 06. 2019 15:27)
Re: Limitny maraton
↑ Marian:
Ahoj
Ta konvergence řady je vidět už z toho,že  .
.
Už ta majoranta bude mít častečný součet  .
.
Co se týče kladnosti,tak řada podobná zadané,jen se střídavými znaménky by měla mít součet nula.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#387 10. 06. 2019 15:03 — Editoval vanok (11. 07. 2019 23:35)
Re: Limitny maraton
Pozdravujem ↑ Marian:,
Presnejsie vyuzil som Riemann-ovu sumu  .
.
Otazka
↑ Marian:
Mozes nam vysvetlit tvoj vysledok, ktory si vyssie v#385 napisal ( a je tu v ramecku pripomenuty).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#388 10. 06. 2019 15:20 — Editoval stuart clark (10. 06. 2019 15:20)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
Problem 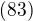
If  for all
for all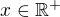 and
and 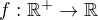 and
and  .
.
Then value of 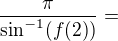
Offline
#389 13. 06. 2019 00:53 — Editoval laszky (13. 06. 2019 01:23)
Re: Limitny maraton
Offline
#390 18. 06. 2019 01:43
#391 24. 06. 2019 00:14
Re: Limitny maraton
Hi ↑ stuart clark:,
this problem (83) is very interesting, but you chose the wrong place to ask it!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#392 24. 06. 2019 15:37 Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš.
#393 06. 07. 2019 22:24
#394 08. 07. 2019 21:42 — Editoval vanok (10. 07. 2019 14:23)
Re: Limitny maraton
Ahoj ↑ kerajs:,
Problem (84).
Poznamka: najrychlejsia metoda je, zda sa mi, vypocet vdaka Stolz-Cesaro-vej vety.
Ty cakas ine riesenie?
POZOR
Poznamka co som napisal vyssie je nepresna.
Pozrite na ↑ vanok:, kde najdete co treba.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#395 09. 07. 2019 07:11
Re: Limitny maraton
↑ vanok:
Svádí to k SC, ale je nutno si uvědomit, že klasické znění tebou navrhované poučky nezahruje případy, kdy jsou všechny sčítance závislé na n.
Jeví se pravděpodobné, že limita bude rovna 1. Možná by to šlo nějak odhadem shora a zdola (ten zdola je triviální). Shora zatím nevím.
Offline
#396 09. 07. 2019 09:16 — Editoval vanok (09. 07. 2019 09:55)
Re: Limitny maraton
Ahoj ↑ Marian:,
Zda sa, ze hladana limita je 1.
No skusme najst dokaz.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#398 10. 07. 2019 14:21 — Editoval vanok (12. 07. 2019 16:59)
Re: Limitny maraton
Cau ↑ Marian:,
Tvoja poznamka je skutocne spravna.
V mojom prispevku ↑ vanok: som sa, trochu urychlene, a nepresne vyjadril.
Tak tu pridavam to co som mal napisat.
Na dokaz, podla mna sa da pouzit znama Caychyho veta, ( z jeho knihy Analyse algébrique z 1821).
Ide o vetu: Ak postupnost 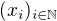 konverguje k nule, tak aj postupnost jej aritmetickych priemerov konverguje k nule.
konverguje k nule, tak aj postupnost jej aritmetickych priemerov konverguje k nule.
Aby sa tu zbytocne nepolemizivalo, pripominam, ze  obsahuje (tuto) aj
obsahuje (tuto) aj  .
.
Pochopitelne je lahke generalizovat tuto vetu aj ked dana limita konverguje k realnemu cislu  . (1)
. (1)
A tiez, ak dana postupnost je kladna aj na jej geometricky priemer. (2) ( tieto generalizacie necham foristom doplnit).
Tak teraz, vdaka tomu, co som tu vyssie napisal, da sa urobit jednoduchy a rychly dokaz. Tak tu dam nan navod.
Pripominam, ze som tu uz dokazal, ![kopírovat do textarea $\sqrt[n]{n} $](/mathtex/1b/1b9f186162fcc9d5a910fad34bcf3472.gif) konverguje k
konverguje k  .
.
No vsak, pridavam este aj dokaz tohto tvrdenia vdaka (2).
Podobne vdaka (1)
![kopírovat do textarea $\lim_{ n \to \infty } \frac{1+ \sqrt{2} + \sqrt[3]{3} +...+ \sqrt[n]{n} }{n} =1$](/mathtex/ab/ab337fa0e8cd32cadf87d3049ce4e07c.gif) lebo
lebo ![kopírovat do textarea $\sqrt[n]{n} $](/mathtex/d2/d2fe3a71ba9381f9e4d4f610eb84f1b5.gif) konverguje k
konverguje k  .
. Édit. Toto nie je riesenie danej otazky... treba ho nast.( dakujem kolegovy Bâti za upozornenie)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#399 12. 07. 2019 12:34
#400 12. 07. 2019 13:00 Příspěvek uživatele vanok byl skryt uživatelem vanok. Důvod: Nepresna odpoved
Stránky: 1 … 14 15 16 17 18 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton
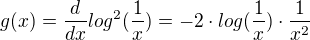
 pre
pre 
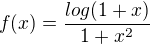
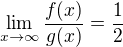 limita je vlastna nenulová
limita je vlastna nenulová![kopírovat do textarea $\int_{K}^{\infty }g(x) dx=[log^{2}(\frac{1}{x})]_{K}^{\infty }=\infty $](/mathtex/53/538338a73d699ec94bfe541cf453a03d.gif)
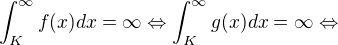


 we deduce that
we deduce that 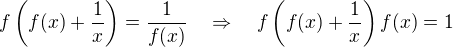 for all
for all 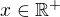 .
. for all
for all 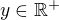 we may set
we may set 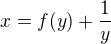 and use it in the previous equality. We obtain
and use it in the previous equality. We obtain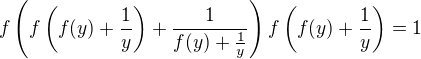 .
.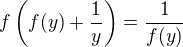 , which results into the relation
, which results into the relation 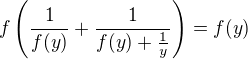 valid for all
valid for all  is increasing, it's invertible and there holds
is increasing, it's invertible and there holds 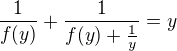 for all
for all 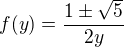 . In order to obtain an increasing function, we choose the minus sign. Hence
. In order to obtain an increasing function, we choose the minus sign. Hence 
 is a length of the side of a regular decagon inscribed in a unit circle, there holds
is a length of the side of a regular decagon inscribed in a unit circle, there holds 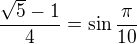 .
. 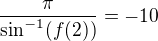 .
.![kopírovat do textarea $\lim_{ n \to \infty } \frac{ \sqrt{n} + \sqrt[3]{n} +...+ \sqrt[n]{n} }{n} $](/mathtex/9d/9d6b5e6b0281d6575d2c4237d895c2ab.gif)
![kopírovat do textarea $\sqrt[n]{n} =\sqrt[n]{1.\frac 21 . \frac 32 ...\frac n{n-1} }$](/mathtex/2c/2cbf2c4020674ba8d2f7e838e852fd0b.gif) konverguje k
konverguje k  konverguje k
konverguje k