Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 … 15 16 17 18 19 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton
#401 12. 07. 2019 14:10
#402 12. 07. 2019 16:03
Re: Limitny maraton
Cau ↑ Bati:,
Presne to iste som ti napisal.
A pytany vysledok je lahko z toho dedukovat. ( ak je to ti co ta trapi), lebo  konverguje k nule.
konverguje k nule.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#403 12. 07. 2019 16:06
#404 12. 07. 2019 16:22 — Editoval vanok (12. 07. 2019 16:23)
Re: Limitny maraton
Co tu pisem je ti jasne?
Tak vidis preco ![kopírovat do textarea $\lim_{ n \to \infty } \frac{1+ \sqrt{n} + \sqrt[3]{n} +...+ \sqrt[n]{n} }{n} =1$](/mathtex/3c/3cdbcde6638b3f35b94a13327853016c.gif) .
.
A tiez, ze 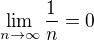 .
.
A tak vyuzi, vetu o rozdiele limit.
(Poznamka : nepouzivam nic ine ako Cauchy v 1821....)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#405 12. 07. 2019 16:29
#406 12. 07. 2019 16:54 — Editoval vanok (12. 07. 2019 17:14)
Re: Limitny maraton
↑ Bati:,
Dakujem za upozornenie.
Som nepozorne cital ( a kopiroval ) text cvicenia.
I ked zatial som dokazal, ze ![kopírovat do textarea $\lim_{ n \to \infty } \frac{1+ \sqrt{2} + \sqrt[3]{3} +...+ \sqrt[n]{n} }{n} =1$](/mathtex/ab/ab337fa0e8cd32cadf87d3049ce4e07c.gif) to nedava odpoved na danu otazku.
to nedava odpoved na danu otazku.
( upravim moju odpoved, aby tam neostali nepresnosti)
A tak ostava stale hladat dokaz daneho tvrdenia, cize ![kopírovat do textarea $\lim_{ n \to \infty } \frac{1+ \sqrt{n} + \sqrt[3]{n} +...+ \sqrt[n]{n} }{n} =1$](/mathtex/3c/3cdbcde6638b3f35b94a13327853016c.gif) .
.
(Ako potvrdil kolega↑↑ kerajs: v prispevku #397 ).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#407 12. 07. 2019 23:27
Re: Limitny maraton
↑↑ vanok:↑↑ Marian:↑↑ kerajs:
Panove, zatim jste nenapsali nic co by me aspon trochu presvedcilo, ze ta limita je 1, takze jsem si to musel spocitat sam. Nejprve nejake odhady:
Pro 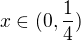 ,
, 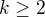 a
a  plati
plati 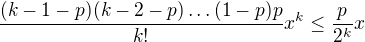 .
.
Dukaz:
Pouzitim odhadu v binomickem rozvoji dostanu
 ,
, 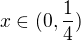
To ted pouziju pro
 (BUNO
(BUNO  ) a
) a  :
: ,
,kde jsem taky pouzil odhad castecneho souctu harmonicke rady. Takze, oznacim-li
![kopírovat do textarea $a_n=\sum_{i=2}^n\sqrt[i]n$](/mathtex/90/90e586262d3fce27108ddf351561ac02.gif) , pak
, pak![kopírovat do textarea $1\leq a_n-a_{n-1}=\sqrt[n]n+\sum_{i=2}^{n-1}(n^{\frac1i}-(n-1)^{\frac1i})\leq\sqrt[n]n+\frac32n^{-\frac12}(\ln(n-1)+1)$](/mathtex/7b/7bea4cebb642747ed2b5ed18ba4921dd.gif) . Z toho vidime, ze
. Z toho vidime, ze  . A protoze
. A protoze  , podle Stolzovy vety dostavame ze
, podle Stolzovy vety dostavame ze 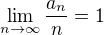 , coz jsme chteli dokazat.
, coz jsme chteli dokazat. Offline
#408 13. 07. 2019 00:21 — Editoval laszky (13. 07. 2019 00:22) Příspěvek uživatele laszky byl skryt uživatelem laszky. Důvod: Byla to holt pekna blbost.
#409 13. 07. 2019 03:13
Re: Limitny maraton
Ahoj ↑ laszky:,
Geometricky priemer je mensi ako aritmeticky.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#410 13. 07. 2019 03:16
#411 15. 07. 2019 19:04
#412 15. 07. 2019 20:02 — Editoval kerajs (15. 07. 2019 21:11)
#413 20. 07. 2019 21:53
Re: Limitny maraton
Problem (86)
Vysetrite dve postupnosti 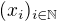 a
a  ak
ak  a
a 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#415 21. 07. 2019 10:38
#416 21. 07. 2019 11:15 — Editoval vanok (21. 07. 2019 11:44)
Re: Limitny maraton
Ahoj ↑ Bati:,
To mas pravdu, ze najprv je dobre ukazat ( napr.), ze pre kazde  ,
, 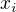 ,
, 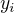 existuju a su v intervale
existuju a su v intervale ![kopírovat do textarea $[0;7]$](/mathtex/8e/8e51a87c005f44130acfe64af32ca7d2.gif) .
.
Potom ukazat, ze ak obidve postupnosti maju limity  ,
,  tak ukazat, ze musi platit
tak ukazat, ze musi platit 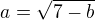
 , a potom vyriesit tento system.
, a potom vyriesit tento system.
A nakoniec doriesit problem ...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#417 21. 07. 2019 12:01 — Editoval krakonoš (21. 07. 2019 12:24)
Re: Limitny maraton
↑ vanok:
Ahoj.
Mně ale vychází,že posloupnost xi je po dvou členech klesající ,pak po dvou opět rostouci,opět klesající po dvou....- jako za sebou zařazenáWWW...
Ukazuje to i indukce,když si vyjádříš podíl xiplus1/xi.Je otázka,zda dochází vůbec k "přibližování" k limitě -"snižování zubů"
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#418 21. 07. 2019 13:04 — Editoval vanok (22. 07. 2019 14:02)
Re: Limitny maraton
Ahoj ↑ krakonoš:,
To pises zaujimave pozorovanie. A iste, by si nasla tvojou cestou tiez
Tu ti napisem, podobnu cestu k tomu rieseniu, ale rozdolenu na tri etapy. (Naznacenu uz v #416)
Tam ta prva etapa ukaze len, ze tie postupnosti su ohranicene. ( a ze ak existuju su konecne).
Druha ukaze ( po rieseni uvedeneho systemu), ze ak tie limity existuju, tak su 2 a 3.
( to vlasne je dokaz v #414, i ked sa to da rychlejsie urobit).
To vsetko ale este nestaci na dokaz tych limit.
To ukaze, dalsie vysetrovanie danych postupnosti.
(Je napr. je mozne urobit vdaka studiu postupnosti  a
a 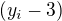 )
)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#419 21. 07. 2019 16:29
#420 21. 07. 2019 18:44
Re: Limitny maraton
Ahoj ↑ kerajs:,
Ano za predpokladu ze limity a, b existuju to si uz v #414 dokazal, ze potom a=2 a b=3, i ked sa to da rychlejsie dokazat ( a lepsie napisat).
No treba este dokazat ako som to vyssie napisal, ze ide o limity definovanych postupnosti v ↑ vanok:.
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#421 21. 07. 2019 21:50 — Editoval vanok (25. 07. 2019 00:32)
Re: Limitny maraton
Riesenie podla ↑ vanok:.
Prvy bod to iste kazdy vie urobit.
Druhy bod. 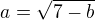
 v pre a, b v [0;7]
v pre a, b v [0;7]
Nam da 
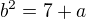
Co sa da ekvivalentne napisat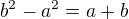 (tato rovnica da
(tato rovnica da  )
)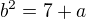
co ( po malych uvahach) da system 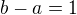
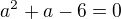
A preto 
Treti bod.
( vysetrime postupnosti  a
a 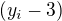 )
)
Zaciatok dokazu:
Hned vidime, ze  a tiez
a tiez 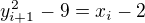
Co da 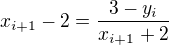 ako aj
ako aj 
a preto ako aj
ako aj 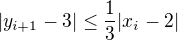
To nam da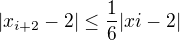
A tak mame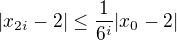 a tiez
a tiez 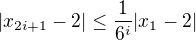
Co da 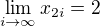 a
a 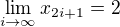 a tak....
a tak....
....dokazete to ukoncit?
Kontrola
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#422 30. 07. 2019 21:28
Re: Limitny maraton
Problem (87).
Vysetrite konvergenciu realnej postupnosti 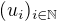 takej, ze
takej, ze  a
a 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#423 31. 07. 2019 00:24
- check_drummer

- Příspěvky: 4637
- Reputace: 99
Re: Limitny maraton
↑ vanok:
Ahoj, hodně neformálně (možná i špatně):
"Máte úhel beta." "No to nemám."
Offline
#424 31. 07. 2019 09:20 Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš.
#425 31. 07. 2019 14:28 — Editoval krakonoš (31. 07. 2019 20:43)
Re: Limitny maraton
↑ vanok:↑ check_drummer:
Ahoj.
Mně příjde,že o růstu či klesání posloupnosti rozhodnou už členy u4-u3, protože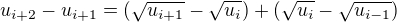 , pokud tedy uvažujeme indukcí.
, pokud tedy uvažujeme indukcí.
Pokud je posloupnost klesající, je zdola omezená svou nezáporností, limita tedy existuje. Protože operací odmocňování se nemůžeme dostat k nulové limitě, vyhovuje pouze limita rovna 4. Tato posloupnost bude tedy zdola omezena svou limitou.
V případě rostoucí posloupnosti se ale ještě nějak musí dokázat omezenost shora.
Pokud bude  , bude limita rovna nule.
, bude limita rovna nule.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
Stránky: 1 … 15 16 17 18 19 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton

![kopírovat do textarea $\{\sqrt[n]n\}_{n=1}^{\infty}$](/mathtex/9e/9eef2a496567d6e22b783c36a625504f.gif) je
je ![kopírovat do textarea $\{\frac{1+\sqrt2+\sqrt[3]3+\ldots+\sqrt[n]n}{n}\}_{n=1}^{\infty}$](/mathtex/d2/d222b89fcde79c0ed0a7f67eec2bd634.gif)
![kopírovat do textarea $\frac{1+ \sqrt{n} + \sqrt[3]{n} +...+ \sqrt[n]{n} }{n} \neq\frac{1+\sqrt2+\sqrt[3]3+\ldots+\sqrt[n]n}{n}$](/mathtex/d9/d91a5a6f22427460ed3f3e2a4c1bfda3.gif)
![kopírovat do textarea $x\leq\frac12\sqrt[k]{x}\sqrt[k]{\frac{k!}{(k-1-p)(k-2-p)\ldots(1-p)}}=R$](/mathtex/26/26365d328b78b284118d52a87e2f1b1b.gif) . Cislo
. Cislo  muzeme odhadnout zesopda:
muzeme odhadnout zesopda: ![kopírovat do textarea $R\geq\frac12\sqrt[k]x\sqrt[k]k\geq\frac12\sqrt x$](/mathtex/16/1611c52ece2cafe9e955efa1a2196914.gif) . Staci tedy aby
. Staci tedy aby 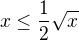 , coz je ekvivalentni
, coz je ekvivalentni  .
.


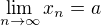 ? Tj. ze existuje a neni nekonecno?
? Tj. ze existuje a neni nekonecno?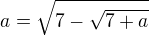 v R (nebo rovnica nema riesenie w R) to potvrdí (popře).
v R (nebo rovnica nema riesenie w R) to potvrdí (popře).
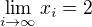 .
.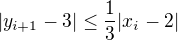 atd..... co da
atd..... co da  .
.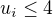 bude toto pro
bude toto pro 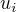 stále platit a totéž pro opačnou nerovnost - takže posloupnost je v těchto případech shora (zdola) omezená a lze ukázat, že i rostoucí (klesající) a snadno se zjistí, že limita je 4.
stále platit a totéž pro opačnou nerovnost - takže posloupnost je v těchto případech shora (zdola) omezená a lze ukázat, že i rostoucí (klesající) a snadno se zjistí, že limita je 4.