Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 17. 09. 2019 11:43 — Editoval vanok (17. 09. 2019 19:16)
Re: limit
Hi ↑ stuart clark:,
Hint: You can also use 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

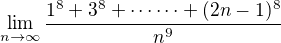
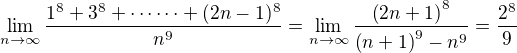
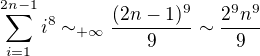 (1) and
(1) and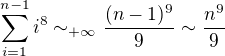 (2)
(2) , we get series of pair terms from series (1) and
, we get series of pair terms from series (1) and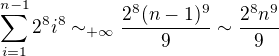 (3)
(3)