Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Sčítání pravděpodobností - sjednocení navzájem se vylučujících jevů
#1 09. 10. 2019 20:11
Sčítání pravděpodobností - sjednocení navzájem se vylučujících jevů
Ahoj,
mám následující příklad:
Dokažte indukcí vzorec pro pravděpodobnost sjednocení  navzájem se vylučujících jevů.
navzájem se vylučujících jevů.
Jedná se o příklad z učebnice matematiky pro gymnázia, jehož řešení tam ale není uvedeno a na netu jsem ho nenašel. Byl bych rád, kdyby mi ho mohl někdo zkontrolovat, popřípadě okomentovat/opravit. Moje řešení je následujíci:
Krok 1:
Pro r=1 platí následuící:
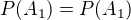
A pro r=2 platí následující:
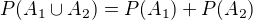
Krok 2:
Předpokládejme, že věta platí pro nějaké 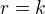 , platí tedy:
, platí tedy:
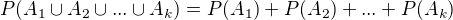
Za tohoto předpokladu dokážeme, že platí věta pro 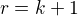 :
:
Víme, že
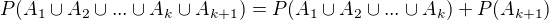
Podle indukčního předpokladu můžeme psát:
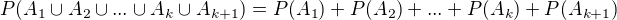
Tím je platnost věty dokázána.
K tomuto příkladu mám dvě následující otázky:
a) Matematická indukce vždy začíná (co já vím) tím, že ukážu, že platnost je zaručena pro 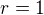 . Lze v tomto případě tento krok přeskočit a začít tím, že platnost platí pro
. Lze v tomto případě tento krok přeskočit a začít tím, že platnost platí pro 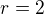 ? Pro
? Pro 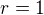 je to jen opsaná rovnost. Jak je to v obecném případě? Čím se začíná?
je to jen opsaná rovnost. Jak je to v obecném případě? Čím se začíná?
b) Na webu jsem našel publikace, ve kterých tento vztah (pro  ) nedokazují a přímo říkají, že to platí. Je to uvedeno jako definice nebo i jako axiom, který se nedokazuje. Je tedy potřeba uvedený vztah opravdu dokazovat? Jaký je rozdíl mezi tím, když si stanovím, že to platí pro dva jevy nebo
) nedokazují a přímo říkají, že to platí. Je to uvedeno jako definice nebo i jako axiom, který se nedokazuje. Je tedy potřeba uvedený vztah opravdu dokazovat? Jaký je rozdíl mezi tím, když si stanovím, že to platí pro dva jevy nebo  jevů? Chápu, že
jevů? Chápu, že  jevy jsou méně než
jevy jsou méně než  jevů a měli bychom jít od elementárních poznatků ke složitějším, ale velký rozdíl v tom tady nevidím a takňák chápu, že když to platí pro 2, tak to musí platit i pro
jevů a měli bychom jít od elementárních poznatků ke složitějším, ale velký rozdíl v tom tady nevidím a takňák chápu, že když to platí pro 2, tak to musí platit i pro  navzájem se vylučujícch se jevů.
navzájem se vylučujícch se jevů.
Offline
#2 10. 10. 2019 11:14
Re: Sčítání pravděpodobností - sjednocení navzájem se vylučujících jevů
↑ Andrew123:
Trvat na tom, že indukce začíná vždy n=1 je nesmysl. Indukce začíná tím krokem, kdy prostě dokazovaný vztah začínä platit. Jde o nastartování jistého řetězce , a pak už stačí obecně předpokládat pro n, dokázat pro n+1.
Nemáme však důkazy jen matematickou indukcí, mnohdy lze použít i přímý např. důkaz. Možná i zde se uvažovalo, že to lze brát i tak, že vezmu dva jevy, ty sjednotím , vznikne tak nový jev, který má svou pravděpodobnost, která je rovna součtu pravděpodobností těch dvou elementárních jevů, takže vlastně mám nový jeden jev s určitou pravděpodobností a přidäm další jev a takto pokračuji.
Co se týče té indukce, píšeš, že to má smysl až od 2 jevů, když je řeč o sjednocení.
Indukci lze podle mě brát i podle počtu sjednocení, kterých je o jednu méně než jevů.
Pak by to začínalo n=1.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Sčítání pravděpodobností - sjednocení navzájem se vylučujících jevů