Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 10. 2019 23:05
Zjednodušení goniometrických výrazů
Dobrý večer, nejméně dvě hodiny trávím čas nad zjednodušením goniometrických výrazů a u níže uvedených dvou příkladů si nevím rady, nejdou mi dopočítat. Moc prosím o pomoc, jak mám dále postupovat. Předem mnohokrát děkuji za Vaši pomoc a strávený čas u mého dotazu...
a) 1+cos2x 1+cos²x-sin²x 1+ (cosx-sinx) x (cosx+sinx)
---------- = -------------- = ------------------------------
sin2x 2sinx x cosx 2sinx x cosx
Došla jsem k tomuto postupu, avšak nevím, jak dále pokračovat. Můžu krátit, ale nevychází mi stále správný výsledek. Výsledek má být cotgx (tedy: cosx )
------
sinx
b) 1-cos2x
-------- = ?
1+cos2x
U tohoto příkladu si pro změnu nevím rady vůbec. Správný výsledek má být tg²x... Ještě jednou předem moc děkuji za pomoc s výpočtem (resp. zjednodušením) obou příkladů.
Offline
#4 26. 10. 2019 23:23
Re: Zjednodušení goniometrických výrazů
↑ SiPe:
Zdravím,
v prvním příkladu nemůžeš krátit, v čitateli máš součet. Postupuj dle rady ↑ Ferdish:: nahraď v čitateli 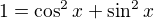 a dostaneš
a dostaneš  . A s tím si už poradíš, ne?
. A s tím si už poradíš, ne?
Ve druhém příkladu postupuj jako u prvního, nahraď 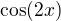 , a pak opět užij
, a pak opět užij 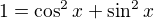
Offline
#7 26. 10. 2019 23:32
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Zjednodušení goniometrických výrazů
↑ SiPe:
Je mi ľúto, kompletné riešenia zo zásady neposkytujem. Je to aj proti pravidlám fóra. Môžem niečo naznačiť, dokončiť však musíte sama.
Príklad a)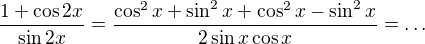
Príklad b)
Offline
#8 26. 10. 2019 23:41
Re: Zjednodušení goniometrických výrazů
Příklad za b) - došla jsem tedy k cos²x +sin²x - cos²x +sin²x
-------------------------------
cos²x +sin²x +cos²x - sin²x
Když to vykrátím, tak mi zůstane: -cos²x + sin²x
----------------
+cos²x - sin²x
A nevím, co dál... má to vyjít tg²x,což tedy absolutně nepobírám.. děkuji za pomoc
Offline
#9 27. 10. 2019 00:11 — Editoval Ferdish (27. 10. 2019 00:13)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Zjednodušení goniometrických výrazů
↑ SiPe:
Ak máte členy v čitateli alebo menovateli oddelené plusom alebo mínusom, nemôžete krátiť: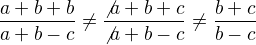
Sčítajte hrušky s hruškami a jablká s jablkami (teda zvlášť sínusy a zvlášť kosínusy) jak v čitateli, tak v menovateli. Až potom budete môcť krátiť, ak bude čo...
Offline
#14 04. 11. 2019 21:11
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Zjednodušení goniometrických výrazů
↑ PAN KOČÍ:
Vitaj na fóre a prečítaj si pravidlá.
Offline

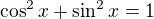
 . Stačí odstranit závorku a upravit. Nakonec v celém zlomku krátit.
. Stačí odstranit závorku a upravit. Nakonec v celém zlomku krátit.