Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#551 22. 11. 2019 18:46
Re: Limitny maraton
Pokracovanie ↑↑ vanok:,
Problem (100) , indikacie:
Mozme vyhodne pouzit, ze ak 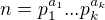 kde
kde  su rozne prvocisla a
su rozne prvocisla a  prirodzene cisla, ze potom
prirodzene cisla, ze potom
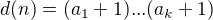 .
.
Tiez moze byt uzitocne pouzit funkciu 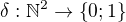 taku, ze
taku, ze ak
ak  deli
deli 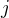 a
a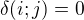 ak
ak  nedeli
nedeli 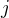 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#552 22. 11. 2019 20:21
Re: Limitny maraton
↑↑ vanok:
Zdravím.
Nevím, jak je tomu dnes, ale v 80tých letech se na matematice studovaly 4 obory(matematická analýza,pravděpodobnost a statistika -tyto dva obory měly první dva roky sloučenou výuku.Podobně numerická matematika a kybernetika).Algebra se učila první tři semestry a lineární algebra první dva semestry.Jako obor se asi dala studovat jen individuálně, i počtem hodin toho bylo méně, zatímco ve druháku byla analýza asi10-12 hodin týdně.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#553 23. 11. 2019 14:04 — Editoval vanok (24. 11. 2019 11:59)
Re: Limitny maraton
Pokracovanie ↑ vanok:,
Cize mame 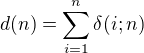 a pochopitelne
a pochopitelne 
(vymenil som riadky a stlpce v trojuholnikovej « tabulke »).
Akoze pre dane i,  je pocet nasobkov cisla i mensich alebo roznych ako n; a je to cislo k take ze
je pocet nasobkov cisla i mensich alebo roznych ako n; a je to cislo k take ze 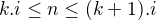 a tak
a tak ![kopírovat do textarea $k=[\frac ni]$](/mathtex/09/09124ef96fa67d5ca068607e78deed33.gif)
( kde [.] je funkcia cela cast), co nam da :
Dokazete to dokoncit?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#554 24. 11. 2019 12:17 — Editoval vanok (24. 11. 2019 12:39)
Re: Limitny maraton
Ukoncenie ↑ vanok:
To znamena ![kopírovat do textarea $u_ n= \frac 1n \sum_{i=n}^{n} [\frac ni]$](/mathtex/97/976e63d83b08c7cede0c1593bbab9f34.gif) a
a 

Cize  .
.
Tak postupnost 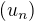 diverguje.
diverguje.
Na druhu otazku pouzijeme
Co da 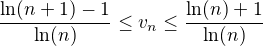 .
.
A tak postupnost 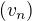 converguje k
converguje k  .
.
To tiez znamena, ze 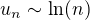 ( u_n je ekvivalentne z ln (n) ).
( u_n je ekvivalentne z ln (n) ).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#556 25. 11. 2019 16:14
Re: Limitny maraton
Hi ↑ stuart clark:,
Look, for example, here
https://math.stackexchange.com/question … 1&lq=1
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#557 11. 12. 2019 10:31 — Editoval stuart clark (11. 12. 2019 10:34)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
↑ vanok: Thanks vanok.
Problem (102) Evaluate 
Offline
#558 11. 12. 2019 13:18
Re: Limitny maraton
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#559 02. 01. 2020 23:53
Re: Limitny maraton
Problem (103).
Vdaka Riemann-ovej sume vyjadrite ![kopírovat do textarea $\lim_{n\to+\infty}\frac {\sqrt[n]{n!}}{n}$](/mathtex/d1/d1226a8f8816f9612a9605c3ab7bb568.gif)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#561 03. 01. 2020 12:09 — Editoval krakonoš (03. 01. 2020 12:14)
Re: Limitny maraton
↑ auditor:
Problem103
Zdravím.
Taky jsem takto postupovala.Ještě jsem pro kontrolu použila Stirlingův vzorec pro n! - jiný adekvátní postup.,nejdou mi psát vzorce,nemám signál.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#562 05. 01. 2020 07:31 — Editoval vanok (05. 01. 2020 07:53)
Re: Limitny maraton
Ahoj ↑ auditor:,
Ano to je dobre riesenie.
Trosicku rychlejsie riesenie sa najde vdaka konstatacii, ze ![kopírovat do textarea $a_n=\sqrt[n]{\frac{n!}{n^n}}$](/mathtex/0d/0d9d72d1ac39a65438b56a9fac91d319.gif) .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#563 10. 02. 2020 08:48
#564 10. 02. 2020 18:42 — Editoval krakonoš (19. 02. 2020 12:49)
Re: Limitny maraton
↑ stuart clark:
(Problem104)
Hi


 uniform convergention on interval (0;1)
uniform convergention on interval (0;1)
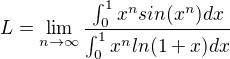
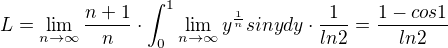
NOTE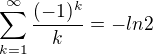
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#565 29. 02. 2020 09:43 — Editoval stuart clark (29. 02. 2020 09:44)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
Thanks ↑ krakonoš:
Problem (105)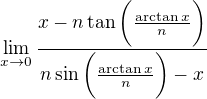 for
for 
Offline
#566 01. 03. 2020 08:53
Re: Limitny maraton
↑ stuart clark:
Hi Stuart Clark., Problem 105
First I used the substitution for arctan x/n, bud there was no limit.
So I have used Maclaurin series for functions. I have got the result  .(if I then numerically somewhere mistaken)
.(if I then numerically somewhere mistaken)
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#567 06. 03. 2020 00:01 — Editoval vanok (06. 03. 2020 00:03)
Re: Limitny maraton
Pozdravujem.
Problem (106).
Vysetrite konvergenciu postupnosti definovanej takto 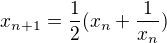 kde
kde 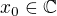 .
.
(Podla Newman, Seminar)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#568 06. 03. 2020 16:49
Re: Limitny maraton
Problem (106).
Mozny navod.
Vyuzite, ze pre  complexne mame
complexne mame 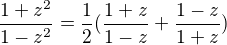 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#569 07. 03. 2020 16:23
Re: Limitny maraton
↑ vanok:
Problem (106).
Teraz mozte urobit zmenu premennych:
polozte 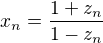 .
.
Vysetrite ako to transformuje vzorec dany v ↑ vanok:?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#570 08. 03. 2020 22:59 — Editoval vanok (10. 03. 2020 10:20)
Re: Limitny maraton
Problem (106).
Kontrola.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#571 17. 03. 2020 10:11
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
Problem (107) : If 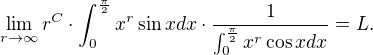 Then
Then 
where  and
and 
Offline
#572 24. 04. 2020 12:42
Re: Limitny maraton
Problem (108).
Nech 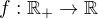 je
je  , taka, ze
, taka, ze  .
.
Co mozte dokazat o  ?
?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#573 25. 04. 2020 09:03
Re: Limitny maraton
↑ vanok:
Pomoc.
Jedna, mozna metoda, je pouzit L’Hôpistal-ove pravidlo.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#574 25. 04. 2020 11:26
Re: Limitny maraton
↑ vanok:
Ahoj.
Já myslela že je to příklad na omezenost funkce,že kdyby měla f(x) konečnou limitu,tak by tam byla omezenost,kde např limita je vlastně jejím supremem, resp infinem,pak by podle mě byla limita derivace této funkce rovna nule, takže by vyhovovala jedině nulová limita fce f.O případu, kdy f(x) nemá smysl uvažovat.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#575 25. 04. 2020 12:21 — Editoval vanok (15. 07. 2020 21:39)
Re: Limitny maraton
Pozdravujem ↑ krakonoš:,
Napisem tak ako to riesit ,( ale su aj ine cesty k rieseniu).
Staci, si uvedomit, ze .
.
A aby som nezabudol, vela zdravia a pekny den.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

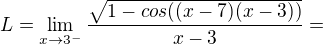
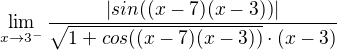

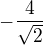

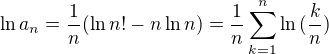
![kopírovat do textarea $\lim_{n\to\infty } \ln{a_{n}}= \int_{0}^{1} \ln{x} {\mathrm{d}}x = [x\ln{x}-x]^{1}_{0} = -1$](/mathtex/9f/9fcf29ccdd425053ad13a86b9525ac26.gif)
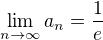


 .
. 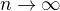


 vtedy su dve mozne situacie: alebo
vtedy su dve mozne situacie: alebo 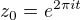 take ze
take ze 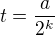 kde a, k su cele a vtedy
kde a, k su cele a vtedy 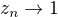 . Ak to tak nie je ,
. Ak to tak nie je , diverguje.
diverguje. 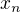 doplnte sami....)
doplnte sami....)