Matematické Fórum

Pomeranc · 08. 01. 2020 18:38 — Editoval jelena (09. 01. 2020 17:08)

Ahoj,

snažila jsem se spočítat nějaké příklady na rezidua a s některými si nevím rady.
a) 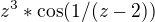$z^{3}*\cos (1/(z-2))$

Je vidět, že tato fce má singularitu ve 2. Když počítám limitu, kde z jde do 2, tak zjistím, že limita neexistuje.
Tedy je to podstatná singularita. Myšlenka byla, že bych to měla rozvést do Laurentovy řady a vzít -1.člen.
Nevím, jestli je to ekvivalentní, ale vzala jsem řadu pro cos x a dosadila 1/(z-2).
Vyšlo mi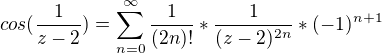
$cos(\frac{1}{z-2})=\sum_{n=0}^{\infty}\frac{1}{(2n)!}*\frac{1}{(z-2)^{2n}}*(-1)^{n+1}$
A pak už jsem si nevěděla rady :(

b) $\frac{e^{z}}{z\cdot (1-e^{-z})}$

Fce má dvě singularity 0 a 2k(Pi)i ,k náleží Z bez 0. 2k(Pi)i je jednonásobný pól, výpočet ok.
0 je dvojnásobný pól a s výpočtem jsem měla problém vzala jsem
$\lim_{z\to0} $\frac{z\cdot e^{z}}{z\cdot (1-e^{-z})}$^\prime= \lim_{z\to0} \frac{e^{z}+z\cdot e^{z}-1}{{(1-e^{-z})^{2}}}$
a přijde mi, že to nějak dál nevede.

Máte nějaký nápad do s tím?

Edit: nějak mi to tu limitu nechce zobrazit. V náhledu to fungovalo, napsala jsem tam toto:
\lim_{z\to0} (\frac{z*e^{z}}{z*(1-e^{-z})})´= \lim_{z\to0} \frac{e^{z}+z*e^{z}-1}{{(1-e^{-z})^{2}}}

Jelena: edit TeX: znak derivace ^\prime, násobení \cdot viz TeX guru Marian + editor TeX napravo od okna zprávy

jelena · 09. 01. 2020 18:07

Zdravím,

u 2. jsem opravovala TeX (souhlasí s tím, co jsi potřebovala zapsat?), výpočet derivace se mi nezdá v pořádku, překontroluj, prosím.
Podstatnější bude využití vzorce pro výpočet rezidua pro pol 2. řádu, zkontroluj, prosím, v materiálech, já bych zapsala jako $\lim_{z\to0} $\frac{(z-0)^2\cdot e^{z}}{z\cdot (1-e^{-z})}$^\prime$ (1/(2-1)! jsem do vzorce nedopsala, ale to jasné). Souhlasí?
Děkuji.

Pomeranc · 09. 01. 2020 19:15

↑ jelena:

Díky, ano, souhlasí to s tím, co jsem chtěla zapsat, matematicky to nesouhlasí, protože jsem se přepsala.
Když jsem zderivovala, ten tvůj správný výraz, tak mi v čitateli vyšlo navíc -2z .

jelena · 09. 01. 2020 22:01

↑ Pomeranc:

dobře, ale i tak mně po úpravě a derivování vychází jinak, upravila jsem na 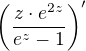$$\frac{z\cdot e^{2z}}{e^{z}-1}$^\prime$ , derivace pro kontrolu WA. Souhlasí? Děkuji.

Pomeranc · 09. 01. 2020 22:39

↑ jelena:

Mně teď wolfram alpha nefunguje, tak jsem to napsala do Mathematicy.
Vyšlo:

//forum.matweb.cz/upload3/img/2020-01/05829_jelena.PNG

Tedy, když jsem se opravila, tak mi to vychází shodně s Mathematicou (viz. do čitatele jsem doplnila -2z).

jelena · 09. 01. 2020 23:11

↑ Pomeranc:

ano, to již se shodujeme. Pro limitu jsem opět použila WA :-) (snad se i Tobě rozběhne, výsledek je 3/2), tipuji, že na 2 l´Hospital to bude dosažitelné.
Je tak? Děkuji.

Pomeranc · 10. 01. 2020 00:52

↑ jelena:

Jj, tím 2* l´H by to mělo jít spočítat. Sice já tam mám numerickou chybu, ale Mathematica s tebou souhlasí.
Wolfram si nefunguje cca 3 měsíce, tedy nejsem moc optimistická, že by se mi měl rozběhnout.

Děkuji za pomoc s příkladem :) .

Bohužel ještě zbývá ten cosinus...

jelena · 10. 01. 2020 17:24

↑ Pomeranc:

Zdravím a také děkuji,
tento WA nefunguje? To by se mi zdálo velmi zvláštní (podrobný postup řešení je, tuším komerční a s registraci, ale výsledek (což pro kontrolu stačí) dává ve 3 prohlížečích a na 2 PC, co jsem teď vyzkoušela). Nemohla jsi nějak nastavit blokování stránky, popř. zkus vyčistit historii a také přidej náhled, co to píše, když nefunguje - nejlépe do sekce pro CAS.

Pro 1. úlohu se podívej do odkazu, je to dost přehledné. Stačí tak? Děkuji.

Pomeranc · 10. 01. 2020 20:21

↑ jelena:

Ano, ten mi nefungoval. Vyzkoušela jsem to i v jiném prohlížeči, tam mi to už šlo.
Do té sekce hodím obrázek, co mi to psalo.

Určitě to stačí. Ten postup se substitucí k tomu výsledku vede.
Ještě jednou děkuji :) .

Matematické Fórum

#1 08. 01. 2020 18:38 — Editoval jelena (09. 01. 2020 17:08)

Výpočet reziduí

#2 09. 01. 2020 18:07

Re: Výpočet reziduí

#3 09. 01. 2020 19:15

Re: Výpočet reziduí

#4 09. 01. 2020 22:01

Re: Výpočet reziduí

#5 09. 01. 2020 22:39

Re: Výpočet reziduí

#6 09. 01. 2020 23:11

Re: Výpočet reziduí

#7 10. 01. 2020 00:52

Re: Výpočet reziduí

#8 10. 01. 2020 17:24

Re: Výpočet reziduí

#9 10. 01. 2020 20:21

Re: Výpočet reziduí

Zápatí