Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 20. 01. 2020 19:17
#3 20. 01. 2020 19:23
- check_drummer

- Příspěvky: 5173
- Reputace: 106
Re: Rekurentní vyjádření posloupnosti
↑ surovec:
Ahoj, co třeba  ?
?
A nebo  ?
?
"Máte úhel beta." "No to nemám."
Offline
#4 20. 01. 2020 19:44
Re: Rekurentní vyjádření posloupnosti
↑ check_drummer:
Víš, co je rekurentní vyjádření? To je vyjádření pomocí předchozího členu (členů). Pokud je to vyjádření pomocí pořadí členu v posloupnosti, jde o vzorec pro n-tý člen. To, co jsi napsal, je de facto vzorec pro n-tý člen.
Offline
#5 20. 01. 2020 19:50
Re: Rekurentní vyjádření posloupnosti
↑ surovec: Ubezpecujem ta, ze ↑ check_drummer: to vie. Jeho prispevok len inymi slovami hovori to, co moj - precitaj si pravidla. Specialne cast o uvedeni vlastneho pokusu o riesenie a popisu, s cim konkretne mas problem. Inak sa dockas toho, ze odpovedajuci vlozi do svojej odpovede asi tolko energie, ako ty do formulacie otazky, ako si prave videl na prispevku ↑ check_drummer:.
Ale aby sme sa teda posunuli - skus vyraz pre  rozlozit na parcialne zlomky.
rozlozit na parcialne zlomky.
Offline
#6 20. 01. 2020 19:55
Re: Rekurentní vyjádření posloupnosti
↑ vlado_bb:
No já právě nevěděl vůbec, jak na to. Proto jsem k tomu nic vlastního nenapsal.
Budiž: rozklad je 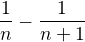 . Ale nechápu, k čemu mi to pomůže...
. Ale nechápu, k čemu mi to pomůže...
Offline
#7 20. 01. 2020 19:59 — Editoval vlado_bb (20. 01. 2020 20:00)
Re: Rekurentní vyjádření posloupnosti
↑ surovec: No a teraz nas zaujima 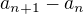 , pripadne
, pripadne 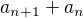 . Ina moznost je vsimnut si podiel dvoch po sebe iducich clenov postupnosti. Neexistuje jednoznacny postup, chce to trochu tvorivosti.
. Ina moznost je vsimnut si podiel dvoch po sebe iducich clenov postupnosti. Neexistuje jednoznacny postup, chce to trochu tvorivosti.
Offline
#8 20. 01. 2020 20:12 — Editoval surovec (20. 01. 2020 20:13)
Re: Rekurentní vyjádření posloupnosti
↑ vlado_bb:
Obávám se, že vůbec nechápu, co tím chceš naznačit... Když to odečtu, mám  , když to sečtu mám
, když to sečtu mám  ...
...
Jak to s tím dál souvisí?
Offline
#9 20. 01. 2020 20:21
Re: Rekurentní vyjádření posloupnosti
↑ surovec: No ale v zadani nie je pozadovana linearna rekurentna formula, alebo ano?
Offline
#10 20. 01. 2020 20:22
#11 20. 01. 2020 20:26
#13 20. 01. 2020 20:45
Re: Rekurentní vyjádření posloupnosti
↑ moab: Elegantne, ale ↑ surovec: sa zrejme uspokoji aj s tym, na co uz sam prisiel, nakoniec aj Wikipedia uvadza na https://en.wikipedia.org/wiki/Recurrence_relation ako rekurentnu formulu  .
.
Offline
#15 20. 01. 2020 20:57
Re: Rekurentní vyjádření posloupnosti
↑ surovec:
Vykašli se na nějaký rozklady na parciální zlomky. Prostě z toho zadaného vzorce vyjádři  (kvadratická rovnice) a pak to dosaď do vzorce pro
(kvadratická rovnice) a pak to dosaď do vzorce pro  .
.
Pokud použiješ dva předchozí členy, dej je do podílu a opět vyjádři  , tentokrát to bude pouze lineární rovnice. A dosaď do vzorce pro
, tentokrát to bude pouze lineární rovnice. A dosaď do vzorce pro  ...
...
Offline
#17 20. 01. 2020 21:47
- check_drummer

- Příspěvky: 5173
- Reputace: 106
Re: Rekurentní vyjádření posloupnosti
A co je špatné na mém druhém vztahu, což je po úpravě ?
?
(a1=1/2)
"Máte úhel beta." "No to nemám."
Offline
#18 20. 01. 2020 21:54
Re: Rekurentní vyjádření posloupnosti
↑ check_drummer:
Jednak to, že  (a tím pádem se druhý a třetí člen odečtou, takže je to pořád jen původní vzorec pro n-tý člen) a druhak to, že (pominu-li fakt v závorce) nejde o rekurentní vyjádření, ale jakýsi hybrid mezi vzorcem pro n-tý člen a rekurentním vyjádřením, který postrádá výhody obou způsobů (člen nespočítám ani pouze z jeho pořadí, ani pouze z předchozího členu) a je tedy k ničemu...
(a tím pádem se druhý a třetí člen odečtou, takže je to pořád jen původní vzorec pro n-tý člen) a druhak to, že (pominu-li fakt v závorce) nejde o rekurentní vyjádření, ale jakýsi hybrid mezi vzorcem pro n-tý člen a rekurentním vyjádřením, který postrádá výhody obou způsobů (člen nespočítám ani pouze z jeho pořadí, ani pouze z předchozího členu) a je tedy k ničemu...
Offline
#19 21. 01. 2020 08:27 — Editoval misaH (21. 01. 2020 10:16)
- misaH
- Příspěvky: 13460
Re: Rekurentní vyjádření posloupnosti
↑ surovec:
No.
Mladý muž, brzdi...
Ja tam vidím napísané, že druhý člen dostaneš tak, že od prvého odrátaš jednu tretinu.
Tretí dostaneš tak, že od druhého odrátaš 1/12.
Čo iné treba?
Všetko tam je...
Keď člen nespočítáš, to je tvoja chyba. Možno si si nevšimol doluuvedenú hodnotu prvého člena... je člen pred členom
je člen pred členom 

Offline
#20 21. 01. 2020 10:49
Re: Rekurentní vyjádření posloupnosti
↑ misaH:
Není mi jasné, co svým příspěvkem chceš říct a na co přesně reaguješ. Každopádně check_drummerovy formule nejsou rekurentní, neboť potřebují k výpočtu znalost POŘADÍ předcházejícího členu. Což jde proti smyslu rekurentního určení posloupnosti – viz tebou uvedená definice.
Offline
#21 21. 01. 2020 11:26 — Editoval jarrro (21. 01. 2020 11:41)
Re: Rekurentní vyjádření posloupnosti
↑ surovec:keď vieš, že chceš počítať 2345. člen prečo by si nemohol využiť poznatok, že ide o 2345. člen? Že niečo závisí (nekonštantne) na niečom inom, neznamená, že to závisí, IBA na tom niečom inom.
(predstav si, že by ti povedali iba, že postupnosť 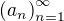 spĺňa
spĺňa  . Vedel by si OKAMŽITE BEZ ROZMÝŠĽANIA zistiť, že ide o postupnosť
. Vedel by si OKAMŽITE BEZ ROZMÝŠĽANIA zistiť, že ide o postupnosť  ?)
?)
MATH IS THE BEST!!!
Offline
#22 21. 01. 2020 12:14
Re: Rekurentní vyjádření posloupnosti
↑ jarrro:
Kdybych měl spočítat 2345. člen pomocí této formule, tak bych musel znát hodnotu 2344. členu. A na ten bych musel znát zase 2343. A tak dále. Docela pracný, ne? Kdybych chtěl 2345. člen, tak prostě vezmu vzorec pro n-tý člen a dosadím, hotovo. A když vím jen nějaký člen (nevím, kolikátý je), tak vezmu rekurentní vyjádření a hnedle mám výsledek. Ten hybrid výše je k ničemu, protože k výpočtu dalšího členu musím mít obě informace (nebo přinejmenším musím jednu z těch informací dopočítat).
Lépe to pochopíš na příkladu:
Je dán (hnusný) hybridní vzorec:
a) Určete 68. člen.
b) Víte, že jeden ze členů posloupnosti má hodnotu 1370. Určete následující člen.
Už rozumíš tomu, jak jsou tyto hybridy nesmyslné?
Offline
#23 21. 01. 2020 12:43 — Editoval Ferdish (21. 01. 2020 12:44)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Rekurentní vyjádření posloupnosti
↑ surovec:
Ale však o tom ti už predsa písala kolegyňa ↑ misaH: v tom vyrezanom odstavci: na určenie ľubovoľného  -tého člena rekurentne určenej postupnosti potrebujeme vedieť/vypočítať VŠETKY predchádzajúce členy, pričom je na začiatku daný len jeden alebo niekoľko prvých členov. Áno, vie to byť pracné, najmä ak je
-tého člena rekurentne určenej postupnosti potrebujeme vedieť/vypočítať VŠETKY predchádzajúce členy, pričom je na začiatku daný len jeden alebo niekoľko prvých členov. Áno, vie to byť pracné, najmä ak je  nejaké vysoké číslo. Ale to je proste vlastnosť rekurentne určenej postupnosti.
nejaké vysoké číslo. Ale to je proste vlastnosť rekurentne určenej postupnosti.
Offline
#25 21. 01. 2020 13:16 — Editoval misaH (21. 01. 2020 13:17)
- misaH
- Příspěvky: 13460
Re: Rekurentní vyjádření posloupnosti
↑ Ferdish:
Ahoj - obávam sa, že zadávateľ absolútne nerozumie pojmu rekurentne zadaná postupnosť.
Údajne všetko sa dá vysvetliť, ale nie každému.
Nech si teda robí , čo chce, on bude škodovať.
Offline
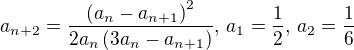

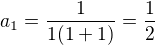

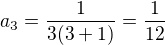
 pomocou matematickej indukcie. Áno, pracné, ale inak to nejde.
pomocou matematickej indukcie. Áno, pracné, ale inak to nejde.