Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 23. 01. 2020 18:18
Re: goniometrická rovnice
↑ vlado_bb:
Ja bych jen podotknul, ze zadavatelka je zrejme zadavatel :D
Offline
#4 23. 01. 2020 18:19
Re: goniometrická rovnice
↑ vlado_bb:
jasný, takže já vlastně řeším, aby argument cosinu se rovnal cos(x)=1, tedy nule. Pak tedy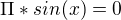
a tedy 
tudíž výsledek je 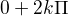 ?
?
Offline
#7 23. 01. 2020 18:26
Re: goniometrická rovnice
↑ vlado_bb:
tak vzhledem k tomu, že sinus nabývá hodnot pouze od -1 do 1, tak v tom případě by taková rovnice neměla řešení, ne?
a oslovení v pohodě, nemáš se za co omlouvat :)
Offline
#9 23. 01. 2020 18:50
Re: goniometrická rovnice
↑ vlado_bb:
super, tak děkuji moc.. a tímto způsobem můžu řešit všechny rovnice, ve kterých budu mít argumentem funkce další funkci :-)
Opravdu děkuji moc, zatím se mějte :)
Offline
#10 23. 01. 2020 18:53
#12 23. 01. 2020 19:04
Re: goniometrická rovnice
Offline
#14 23. 01. 2020 19:16 — Editoval Dáda78 (23. 01. 2020 19:18)
#16 23. 01. 2020 20:36
Re: goniometrická rovnice
↑ vlado_bb:
super.. v souvislosti s tím mě napadá, jak by se řešilo, pokud by to nebyla rovnice, ale nerovnice, například že musí být větší než 0.. zjistil bych si, kdy se rovná výraz nule a poté?
Offline
#17 23. 01. 2020 21:06 — Editoval surovec (23. 01. 2020 21:06)
Re: goniometrická rovnice
↑ Dáda78:
Funkce je periodická po  , takže bych nanesl několik sousedních řešení, která na sebe navazují, na osu v rozmezí intervalu o délce alespoň jedno
, takže bych nanesl několik sousedních řešení, která na sebe navazují, na osu v rozmezí intervalu o délce alespoň jedno  a otestoval bych intervaly. Tady jsou nulové body
a otestoval bych intervaly. Tady jsou nulové body 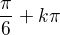 a
a 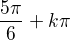 , takže k otestování jsou intervaly
, takže k otestování jsou intervaly 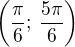 a
a 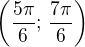 . První je zápornej, druhej kladnej, takže řešením by byly intervaly
. První je zápornej, druhej kladnej, takže řešením by byly intervaly 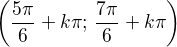 .
.
Offline
#18 23. 01. 2020 21:27
Re: goniometrická rovnice
↑ Dáda78:Vseobecne, ak mame nerovnicu 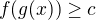 , tak najprv zistime, pre ktore
, tak najprv zistime, pre ktore  je
je 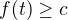 . Nech
. Nech  je mnozina vsetkych takych
je mnozina vsetkych takych  . No a potom zistime, kedy je
. No a potom zistime, kedy je 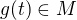 . Jedno ani druhe nemusi byt jednoduche (ani mozne), zavisi to od konkretnych
. Jedno ani druhe nemusi byt jednoduche (ani mozne), zavisi to od konkretnych 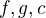 .
.
Offline

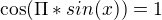
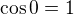 , ale aj napriklad
, ale aj napriklad 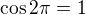 (a nielen to). Vies co s tym?
(a nielen to). Vies co s tym?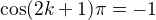
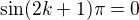
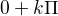 ?
?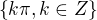 .
.