Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 01. 2020 18:10
Dukaz vlastnosti n-te odmocniny
Ahoj,
mam dotaz k elementarnim dukazum odmocniny. V ucebnici k prikladu nejsou vysledky/reseni, tak bych chtel nekoho poprosit, zda by na to kouknul a popripadne opravil, protoze ve skole jsme to nepocitali. Jedna se o nasledujici 4 obdobne varianty:
Dokazte tyto vety:
a) pro vsechna  je
je ![kopírovat do textarea $\sqrt[n]{0}=0$](/mathtex/c5/c54469ec43a03fda009459563b4b1890.gif) .
.
b) pro vsechna  je
je ![kopírovat do textarea $\sqrt[n]{1}=1$](/mathtex/f9/f980e7ad85663ad72b0bf53de07749f3.gif) .
.
c) pro vsechna 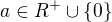 je
je ![kopírovat do textarea $\sqrt[n]{a}=a$](/mathtex/e4/e42769374bec870d201a8c9fd0b62118.gif) .
.
d) pro vsechna  a pro vsechna
a pro vsechna  je
je ![kopírovat do textarea $\sqrt[n]{a}>0$](/mathtex/21/21f8408dab60d85e362bc9a621c35e75.gif) .
.
Me reseni:
a) Plati nasledujici definice: Pro libovolné  definujeme n-tou odmocninu z nezáporného reálného čísla
definujeme n-tou odmocninu z nezáporného reálného čísla  jako nezáporné reálné číslo
jako nezáporné reálné číslo  , pro ktere plati
, pro ktere plati 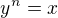 , coz znacime jako
, coz znacime jako ![kopírovat do textarea $\sqrt[n]{x}=y$](/mathtex/55/55f725eecbbd16b15bcc983dc8c47d66.gif) . Dukaz bych provedl podle definice, cili nasledovne. 0 je nezaporne realne cislo, takze to vyhovuje definici a muzeme proto psat specialni pripad, ze
. Dukaz bych provedl podle definice, cili nasledovne. 0 je nezaporne realne cislo, takze to vyhovuje definici a muzeme proto psat specialni pripad, ze 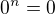
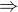
![kopírovat do textarea $\sqrt[n]{0}=0$](/mathtex/c5/c54469ec43a03fda009459563b4b1890.gif) . Hotovo.
. Hotovo.
b) obdobne jako a), tj. podle definice napiseme, 1 je realne nezaporne cislo, takze plati 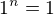 , coz znacime jako
, coz znacime jako ![kopírovat do textarea $\sqrt[n]{1}=1$](/mathtex/f9/f980e7ad85663ad72b0bf53de07749f3.gif) . Hotovo.
. Hotovo.
c) obdobne jako a) a b). 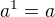 , coz znacime take jako
, coz znacime take jako ![kopírovat do textarea $\sqrt[1]{a}=a$](/mathtex/c4/c41079ecf7b01544fe81d82f9eff34cd.gif) . Hotovo.
. Hotovo.
d) Neni co dokazovat. Primo v definici se uvadi, ze je y nezaporne cislo. Hotovo.
Je to jen moje reseni.. Prijde mi taknak, ze jsem vlastne nic nedokazal.., protoze mi prijdou dokazovane vlastnosti zrejme.. Je myslenka dukazu spravna?
Diky
A.
Offline
#2 24. 01. 2020 19:00
Re: Dukaz vlastnosti n-te odmocniny
↑ Andrew123: Je to v poriadku, len v bode c mas v zadani preklep, namiesto  ma zrejme byt
ma zrejme byt  .
.
Offline
#3 24. 01. 2020 22:06 — Editoval MichalAld (25. 01. 2020 00:06)
Re: Dukaz vlastnosti n-te odmocniny
Podle mě důkaz bodu b) není tak jednoduchý ... a osobně bych řekl, že to vlastně dokázat nejde. Protože třeba ![kopírovat do textarea $\sqrt[2]{1}$](/mathtex/3e/3e82044d0325dd09818313fef1ebf48a.gif) může být stejně tak dobře 1 jako -1, a nelze nijak dokázat, co z toho je pravda ... muselo se to zvolit dohodou...
může být stejně tak dobře 1 jako -1, a nelze nijak dokázat, co z toho je pravda ... muselo se to zvolit dohodou...
Pokud bychom uvažovali i komplexní čísla, podaří se nám pro ![kopírovat do textarea $\sqrt[n]{1}$](/mathtex/fa/fa1f8643440232818379969b90f234e9.gif) najít dokonce n takových čísel, která po umocnění na n-tou dají jedničku. Ale beru, že se můžeme bavit jen o reálných číslech - nicméně ten problém s +- jedničkou pro sudé odmocniny tu zůstává...
najít dokonce n takových čísel, která po umocnění na n-tou dají jedničku. Ale beru, že se můžeme bavit jen o reálných číslech - nicméně ten problém s +- jedničkou pro sudé odmocniny tu zůstává...
To samé je vlastně bod d)
Offline
#4 25. 01. 2020 21:11
Re: Dukaz vlastnosti n-te odmocniny
↑ vlado_bb:
Ahoj, je to opravdu preklep a diky za feedack..:-)
Offline
#5 25. 01. 2020 21:33
Re: Dukaz vlastnosti n-te odmocniny
↑ MichalAld:
Ahoj, dekuji za tvuj komentar. Mohl bys prosim vice rozvest tu situaci v b), respektive d)? Myslis to tak, ze by melo byt spravne v zadani neco jako "Dokazte, ze pro kazdou sudou odmocninu z 1 je 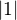 "? Protoze pro liche odmocniny se to stat nemuze.. Jinak ten priklad je z te klasicke ucebnice pro gymnazia Funkce - nakladatelstvi Prometheus, autor Odvarko. Priklad nema hvezdicku, takze neni zarazen ani jako obtizny, takze nevim, proc to maji napsano takhle.
"? Protoze pro liche odmocniny se to stat nemuze.. Jinak ten priklad je z te klasicke ucebnice pro gymnazia Funkce - nakladatelstvi Prometheus, autor Odvarko. Priklad nema hvezdicku, takze neni zarazen ani jako obtizny, takze nevim, proc to maji napsano takhle.
Offline
#6 25. 01. 2020 22:22
Re: Dukaz vlastnosti n-te odmocniny
↑ Andrew123:
Já nevím, já nejsem matematik...jen tuším, že žádný důkaz toho, že  je zrovna 1 a né -1 nemůže existovat, že to bylo zvoleno dohodou...
je zrovna 1 a né -1 nemůže existovat, že to bylo zvoleno dohodou...
V matematice (narozdíl od programovacích jazyků) musí funkce "vracet" jen jednu hodnotu ... takže se z těch dvou musela jedna vybrat (a přirozeně to byla ta kladná). Ale vůbec nic by se nejspíš nestalo, kdyby se vybrala ta záporná...
Stejný problém má i mnoho jiných inverzních funkcí, vlastně vždycky, když původní funkce není prostá ... tj když dvěma různým x přiřazuje stejné y. Například sin(x).
Offline
#8 26. 01. 2020 06:45 — Editoval misaH (26. 01. 2020 06:46)
- misaH
- Příspěvky: 13459
Re: Dukaz vlastnosti n-te odmocniny
↑ MichalAld:
Ahoj.
Vychádza sa čiste z definície.
Odmocnina z prirodzených čísel nie je záporná nikdy. Z definície.
... odmocninu z nezáporného reálného čísla
jako nezáporné reálné číslo
, ...
Offline
#9 26. 01. 2020 08:29
Re: Dukaz vlastnosti n-te odmocniny
MichalAld napsal(a):
třeba
může být stejně tak dobře 1 jako -1, a nelze nijak dokázat, co z toho je pravda ... muselo se to zvolit dohodou...
Presne tak, ta dohoda je definicia. Druha odmocnina z 1 je 1.
Offline

 , pak je tudíž jasné, že x nemůže být menší než 0.
, pak je tudíž jasné, že x nemůže být menší než 0.