Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 01. 2020 03:16
- Budulinek123

- Zelenáč
- Příspěvky: 10
- Reputace: 0
Kolik existuje součtů
Dobrý den, nevim si rady s touto úlohou:
Jediné, co mě napadlo je, že bych to mohl řešit permutacemi s opakováním, kdy jednotlivé disjunktní případy budou:
Pokud mám jedno  , tak zbytek
, tak zbytek 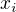 budou 1, to jsou tedy 4 možnosti pro
budou 1, to jsou tedy 4 možnosti pro  .
.
Pokud mám jedno  , tak zbytek budou dvě 1 a jedna 2. To mám tedy
, tak zbytek budou dvě 1 a jedna 2. To mám tedy 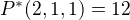 možností. (23 + 2 + 1 + 1)
možností. (23 + 2 + 1 + 1)
Pokud mám jedno  , tak mám buď (22 + 3 + 1 + 1) nebo (22 + 2 + 2 + 1), tedy
, tak mám buď (22 + 3 + 1 + 1) nebo (22 + 2 + 2 + 1), tedy 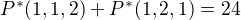 možností.
možností.
Tohle je ale hodně zdlouhavé, nejde to vyřešit nějakým jiným způsobem?
Děkuji
Offline
#2 31. 01. 2020 03:34
#3 31. 01. 2020 05:02
- Budulinek123

- Zelenáč
- Příspěvky: 10
- Reputace: 0
Re: Kolik existuje součtů
Sakra, to jsem nějakým záhadným způsobem úplně přehlédnul.
Ale stejně, jediné co mě napadlo jsou ty disjunktní případy permutací, pro  by to bylo:
by to bylo:
(21+2+2+2)=27 -> 4m.
(20+3+2+2)=27 -> 12m.
(19+3+3+2)=27 -> 12m.
(19+4+2+2)=27 -> 12m.
(18+3+3+3)=27 -> 4m.
(18+4+3+2)=27 -> 24m.
(18+5+2+2)=27 -> 12m
atd...
Offline
#4 31. 01. 2020 06:31 — Editoval laszky (01. 02. 2020 00:36)
Re: Kolik existuje součtů
↑ Budulinek123:
Nápověda: Využij multi-indexů:
Počet multi-indexů  z prostoru
z prostoru 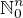 , jejichž délka splňuje
, jejichž délka splňuje 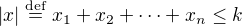 je roven
je roven 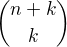 .
.
1) Urči počet multi-indexů 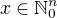 , jejichž délka splňuje
, jejichž délka splňuje 
2) Využij toho, že každý multi-index délky  splňující navíc podmínku
splňující navíc podmínku  odpovídá nějakému multi-indexu délky
odpovídá nějakému multi-indexu délky 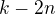 .
.
Offline
#5 31. 01. 2020 14:34
Re: Kolik existuje součtů
Ahoj ↑ Budulinek123:,
Mozes si precitat napr. toto https://math.stackexchange.com/question … nctio?rq=1
Moze to byt uzitocne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 31. 01. 2020 19:45
- Budulinek123

- Zelenáč
- Příspěvky: 10
- Reputace: 0
Re: Kolik existuje součtů
Díky za pomoc, nevěděl jsem že existuje něco jako stack overflow pro matematiku.
Teorii multi-indexů si budu muset znova prostudovat, neboť výše zmíněné odpovědi moc nerozumím.
Offline
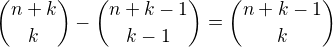

 . Chces-li spocitat jen ty multi-indexy, pro ktere plati
. Chces-li spocitat jen ty multi-indexy, pro ktere plati 
 .
.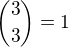 multi-index, a to x=(2,2,2,2). Obdobne pro k=9, existuji celkem 4 multi-indexy. Atd.
multi-index, a to x=(2,2,2,2). Obdobne pro k=9, existuji celkem 4 multi-indexy. Atd.