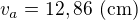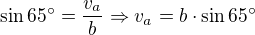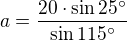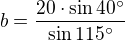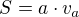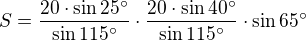Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 01. 2020 20:51
Výška v rovnoběžníku
Dobrý den, potřebuji vypočítat výšku rovnoběžníku, abych zjistila obsah (S= av).
Z rovnoběžníku jsem si vytáhla trojúhelník, jehož délky stran jsou: a=14,2 cm; b= 10 cm; c= 9,3 cm
Zkoušela jsem vypočítat výšku přes Euklidovy věty, vyšla mi 15,6 cm, při vynásobení se stranou a mi ale nevyjde 119,6 cm2, což má být správný výsledek.
Moc děkuji za Váš čas a pomoc!
Offline
- (téma jako vyřešené označil(a) gadgetka)
#3 31. 01. 2020 21:17
Re: Výška v rovnoběžníku
V rovnoběžníku ABCD je dáno IACI = 20 cm, I∢CABI= 40 stupňů, I∢ACBI= 25 stupňů. Vypočtěte délky stran rvnoběžníku a obsah rovnoběžníku.
Délky stran (viz. výše) by měly být vypočítány správně, shodují se s výsledky v učebnici. Jen pořád nemohu přijít na tu výšku, abych dopočítala obsah.
Děkuji za pomoc!
Offline
#4 31. 01. 2020 21:35 — Editoval gadgetka (31. 01. 2020 21:41)
Re: Výška v rovnoběžníku
Zdravím, strany vypočítáš sinovou větou, znáš úhlopříčku tupého trojúhelníku (polovina rovnoběžníku) a dva úhly. Dopočítáš třetí úhel a použiješ sinovou větu. Pro výpočet výšky  si představ rovnoběžník jako rovnoběžky proťaté příčkou, tím spočítáš např. úhel u vrcholu
si představ rovnoběžník jako rovnoběžky proťaté příčkou, tím spočítáš např. úhel u vrcholu  a výška spuštěná z vrcholu
a výška spuštěná z vrcholu  ti vytvoří pravoúhlý trojúhelník
ti vytvoří pravoúhlý trojúhelník 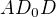 , kde
, kde 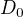 je pata výšky a znáš stranu b. Stačí použít jednu z goniometrických funkcí ostrého úhlu a je hotovo. :)
je pata výšky a znáš stranu b. Stačí použít jednu z goniometrických funkcí ostrého úhlu a je hotovo. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#7 31. 01. 2020 22:09
Re: Výška v rovnoběžníku
Mám to nakreslené přesně jak vy ten trojúhelník ABC. Ale pořád nechápu, jak z toho vypočítám výšku? Goniometrické funkce ostrého úhlu neznám, nedělali jsme to. Pomocí Euklidových vět to nejde, tak fakt nevím co s tím...
Bohužel ani Vašemu vysvětlení nerozumím... Stačil by mi vzoreček, jak z toho trojúhelníku ABC dostanu výšku
Offline
#10 31. 01. 2020 22:45 — Editoval gadgetka (31. 01. 2020 22:51)
Re: Výška v rovnoběžníku
Případně si ten pravoúhlý trojúhelník můžeš dokreslit takto:
P. S. Goniometrické funkce ostrého úhlu se berou už na základní škole, kde se to možná probírá pod názvem goniometrické funkce v pravoúhlém trojúhelníku, ale jde o totéž. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#11 31. 01. 2020 23:01 — Editoval gadgetka (31. 01. 2020 23:05)
Re: Výška v rovnoběžníku
A ještě maličkost, když sis zvolila stejný trojúhelník ABC jako já, strany v něm nemůžou být tyto: a=14,2 cm; b= 10 cm; c= 9,3 cm, protože strana AC je zadaná, to je ta úhlopříčka rovnoběžníku. Strana |AB|=9.33 cm a strana |BC|=14,18 cm. :) ... teď mi došlo, že ses zřejmě jen přepsala, viď? Místo 20 jsi napsala 10... :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline