Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 02. 2020 17:06
Chyba ve zjednodušení rovnice
Zdravím.
Nevíte, kde mám chybu?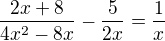
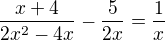
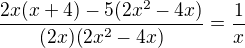
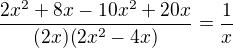
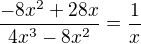
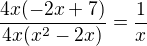
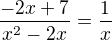
vynásobím celou rovnici: 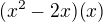
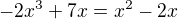
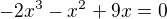
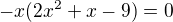
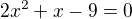
což už teď je špatně, protože diskriminant nulový nebude a výsledek má být 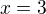 .
.
Vím, že celá rovnice se dá vypočítat jednodušeji a snažím se, ale když se potom dostanu do podobné situace, tak bych rád věděl, kde mám chybu kvůli budoucím výpočtům.
Děkuji moc!
Offline
#7 09. 02. 2020 19:41 — Editoval misaH (09. 02. 2020 19:49)
- misaH
- Příspěvky: 13459
Re: Chyba ve zjednodušení rovnice
↑ vlado_bb:
No - pochopila som to zle... :-)
Brala som prvý riadok ako úplne prvý, hehe...
A divila som sa, že tam žiadne prevádzanie nie je.
No ale tak má to potvrdené, chyba je triviálna...
Pre zadávateľa:
Pri hľadaní spoločného menovateľa rozkladaj radšej najprv menovatele na súčin a potom dopĺňaj čo treba. V tejto rovnici to až tak neprekážalo, ale môže sa ti stať, že po zbytočne krkolomnom menovateli rovnicu nebudeš vedieť doriešiť.
Spoločný menovateľ zo 16 a 32 tiež nie je výhodné mať 16*32, stačí 32 a rátaš s menšími číslami = s menšími chybami (obyčajne)...
Offline
#9 09. 02. 2020 19:46 — Editoval misaH (09. 02. 2020 19:47)
- misaH
- Příspěvky: 13459
Re: Chyba ve zjednodušení rovnice
↑ vlado_bb:
Tak, tak, ale veľa by som na to nevsadila, napríklad vzhľadom k spoločnému menovateľu a úprave rovnice......
Offline

 , nie
, nie 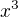 . Ale uz v uvodnom odcitani zlomkov sa dalo postupovat jednoduchsie - spolocny menovatel je
. Ale uz v uvodnom odcitani zlomkov sa dalo postupovat jednoduchsie - spolocny menovatel je 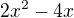 .
.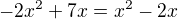
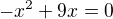
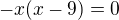
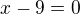


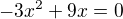

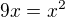
 a mal by vediet zdovodnit, ze nula riesenim povodnej rovnice nie je.
a mal by vediet zdovodnit, ze nula riesenim povodnej rovnice nie je.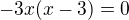
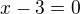
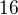 a
a  můžu udělat
můžu udělat 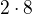 a
a 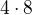 .
. a při druhém jmenovateli nechá
a při druhém jmenovateli nechá  , chápu to správně?
, chápu to správně?