Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 24. 02. 2020 18:47
Re: Zotrvačnosť zrýchlenia
Zrychlení je prostě rychlost změny rychlosti.
Jiná věc je, zda nějakou setrvačnost vykazují věci, které sílu a z ní plynoucí zrychlení řídí v tom dopravním prostředku. A to je dost běžná věc s cílem aby se ovládání nechovalo "jak splašená koza". Pak taky stojící a naklánějící se člověk není zrovna přesný měřič časových průběhů dějů.
Offline
#3 26. 02. 2020 11:55 — Editoval ferit86 (26. 02. 2020 11:56)
Re: Zotrvačnosť zrýchlenia
edison napsal(a):
Zrychlení je prostě rychlost změny rychlosti.
Experiment je proste realita, a zjednodušené definície fungujú na papieri.
edison napsal(a):
Jiná věc je, zda nějakou setrvačnost vykazují věci, které sílu a z ní plynoucí zrychlení řídí v tom dopravním prostředku. A to je dost běžná věc s cílem aby se ovládání nechovalo "jak splašená koza". Pak taky stojící a naklánějící se člověk není zrovna přesný měřič časových průběhů dějů.
Pri malej rýchlosti, pôvodne ubrzdenej z veľkej rýchlosti, ešte chvíľu cítiť dosť veľkú silu. Nedá sa to vysvetliť znemou rýchlosti, pretože tam už skoro žiadna nie je.
Offline
#4 26. 02. 2020 13:38 — Editoval KennyMcCormick (26. 02. 2020 13:39)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Zotrvačnosť zrýchlenia
Nedá sa to vysvetliť znemou rýchlosti, pretože tam už skoro žiadna nie je.
To je dobrá otázka. Jak může být velká změna rychlosti, pokud je rychlost velice malá?
Jednoduše. Velká změna veličiny neimplikuje velkou veličinu jako takovou.
Ukážu ti to na příkladě. Představ si funkci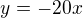 .
.
Tohle je funkce, která vypadá takhle:
.
Změna x je v tomto případě -20 úplně všude. (To je proto, že je to přímka - ať na té přímce ukážeš kamkoli, všude platí, že když postoupíš o jeden krok doprava, nastane změna o 20 kroků směrem dolů.)
A teď se podívej např. na bod x = -0,01. Vidíš, že tam je taky změna x rovna -20 (protože je rovna -20 úplně všude).
A to je odpověď na otázku, jak můžeš mít velice malou rychlost, ale velkou změnu rychlosti.
(Dá se to napsat i matematicky, ale tím bych ti to asi nekomplikoval...)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#5 26. 02. 2020 14:20
Re: Zotrvačnosť zrýchlenia
Existuje spousta přístrojů, které používají akcelerometry jako součást principu činnosti. Kdyby zrychlení nebyl prostý poměr dv/dt, všechny tyhle věci (včetně řídících systémů raket a pod.) by prostě nefungovaly. Jelikož normálně fungují, dá se očekávat, že diskutovaný jev je jen jeden z mnoha typů smyslových klamů.
Offline
#6 26. 02. 2020 20:09
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Zotrvačnosť zrýchlenia
Ještě to možná může být ryv. 🙂
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#7 27. 02. 2020 15:06 — Editoval ferit86 (27. 02. 2020 15:17)
Re: Zotrvačnosť zrýchlenia
↑ KennyMcCormick: Ďakujem, znie to logicky. Postavil som sa a dal nohy od seba pol metra. Prudko som sa naklonil a zastal, svaly sa zasekli, bol to podobný pocit ako vo vlaku. Aj tak by som to chcel zmerať akcelerometrom.
↑ edison: Akcelerometre neporovnávajú údaje s kamerou, a nemajú možnosť odlišiť brzdnú silu od iných síl. To si zas len tak typol aby reč nestála? :-)
Offline
#8 27. 02. 2020 17:58
Re: Zotrvačnosť zrýchlenia
Co se změřenými daty děláš ty a co s nimi dělají lidé, kteří vyrábějí fungující věci, může být rozdíl.
Mě by třeba zajímalo, jak by podle tebe měla vypadat ta tvoje setrvačnost zrychlení třeba při dopadu upuštěného předmětu na podlahu. Konvenční závěr je, že po dobu desetin milisekundy působí zrychlení několik tisíc G a pak nic. Jak to probíhá podle tebe?
Offline
#9 27. 02. 2020 18:06
Re: Zotrvačnosť zrýchlenia
Pak je teda otázka, co je vlastně cílem této diskuse. Zeptal ses, zda má zrychlení setrvačnost. Dostal jsi odpověď že ne. Tím je hotovo. Případně může být zajímavé diskutovat o tom, co způsobuje, že tento pocit setrvačnosti máš.
Ale nepočítej s tím, že kohokoli, kdo rozumí fyzice přesvědčíš o opaku. Maximálně tak dostaneš banána když budeš moc otravnej:-) Takových už tu bylo... Zajímavé je, že většina psala slovensky.
Offline
#12 29. 02. 2020 20:36
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Zotrvačnosť zrýchlenia
Postavil som sa a dal nohy od seba pol metra. Prudko som sa naklonil a zastal, svaly sa zasekli, bol to podobný pocit ako vo vlaku. Aj tak by som to chcel zmerať akcelerometrom.
Ryv je změna zrychlení, takže se podíváš, jak rychle se mění zrychlení na akcelerometru, a to je ryv.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#13 01. 03. 2020 11:20
- Tomáš Vencl

- Příspěvky: 94
- Reputace: 4
Re: Zotrvačnosť zrýchlenia
Je tu ještě jeden efekt.
Mezi Vaším vestibulárním aparátem (měřákem zrychlení) a bržděnými koly je spousta pružných členů (odpružení, sedačky, tělo..). Jakmile kola začnou brzdit, setrvačná síla tyto pružné členy vychýlí a deformuje.(akumuluje se tam nějaká energie). V okamžiku, kdy kola na podložce zastaví se výchylka pružných členů začne vracet zpět (do své statické rovnovážné polohy, může to i několikrát zakmitat) a Váš měřák zrychlení na pružném členu ještě nějakou dobu registruje brzdné zrychlení (které plynule klesá k nule, nebo nějak zakmitá, to už záleží na vlastnostech soustavy).
Offline
#14 03. 03. 2020 15:30
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Zotrvačnosť zrýchlenia
To je asi částečně totéž jako efekty ryvu.
physical systems experience oscillations and deformations as a result of jerk
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#15 03. 03. 2020 20:30
- zvedavy123

- Zelenáč
- Příspěvky: 16
- Reputace: -1
Re: Zotrvačnosť zrýchlenia
↑ KennyMcCormick: Vo vlaku je vodorovne-pružný člen nárazník medzi vozňami.
Offline