Matematické Fórum

Dobrý den,
prosím o radu s tímto příkladem: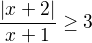 v R

Definiční  obor je R bez -1.

Nulový bod absolutní hodnoty je -2 a nulový bod jmenovatele je -1. Proto jsem si rozdělila řešení příkladu na tři intervaly:
a) (-nekonečno, -2)
b) <-2, -1)
c) (-1, + nekonečno)

V prvním intervalu je absolutní hodnota záporná, proto bude příklad: 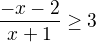. Trojku si zprava převedu na levou stranu a převedu na společný jmenovatel. Budu mít proto 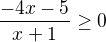. Grafickým řešením zjišťuji, že to vyhovuje intervalu <-5/4, -1), ale řeším na intervalu (- nekonečno, -2). Tedy za a) nemá nerovnice řešení.

Obdobně pokračuji i v případě b). Zde je absolutní hodnota nezáporná, proto ji mohu odstranit, trojku převést na levou stranu a převést na společný jmenovatel. Vznikne mi tak nerovnice 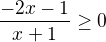. Grafickým řešením získávám interval (-1, -1/2>. Ale řeším na intervalu <-2, -1). Takže i zde nemá nerovnice řešení.

V případě c) získávám stejnou nerovnici. I stejný interval (-1, -1/2>. Navíc řeším v intervalu (-1, + nekonečno). Průnikem je tedy interval  (-1, -1/2>.

Pokud sjednotím všechny obory pravdivosti Pa, Pb, Pc, získám obor pravdivosti P= (-1, -1/2>

Mohu se prosím zeptat, zda počítám správně? Nalezla jsem více možností řešení a nevím, zda je tento správný nebo ne. Někteří řešitelé nerozdělují intervaly b) a c). Ale jiní oponují, že pokud ho nerozdělí, tak dochází k hrubé chybě. Moc děkuji za rady.