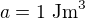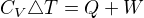Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 03. 2020 05:06
Kruhový děj
Dobrý den,
mohu poprosit o nakopnuti, jak na tento příklad? Ideální dvouatomový plyn podrobí e parabolické expanzi 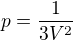 z objemu
z objemu 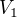 a tlaku
a tlaku 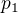 na objem
na objem 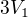 a tlak
a tlak 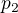 . Určete obecně práci výkonu plynem při dějí a teplo přijaté plynem. Jak v tomto případě urcim, zda jde o izotemicky či adiabaticky děj?
. Určete obecně práci výkonu plynem při dějí a teplo přijaté plynem. Jak v tomto případě urcim, zda jde o izotemicky či adiabaticky děj?
Offline
- (téma jako vyřešené označil(a) Kája2)
#3 30. 03. 2020 17:25
Re: Kruhový děj
↑ MichalAld:
Dobrý den, děkuji. Tudíš bych určil práci takto: 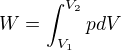 ?Ale s teplem popravdě nevím.
?Ale s teplem popravdě nevím.
Offline
#5 30. 03. 2020 22:24
Re: Kruhový děj
Kdybych to mel pocitat ja, asi bych urcil praci zminenym integralem, ze stavove rovnice dopocital zmenu teploty, z ni zmenu vnitrni energie a z 1.PT pak teplo. To by snad melo jit, ne?
Hlavne jsem ale chtel upozornit, ze ve vztahu 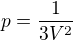 nesedi jednotky.
nesedi jednotky.
Offline
#10 31. 03. 2020 12:37
Re: Kruhový děj
↑ zdenek1:
Dobrý den,
zadání jsem opsal vskutku celé. Pokud tedy dosadím upravený vztah, postup zůstává stejný, jne se trochu změní ty výrazy,že?
Offline
#11 31. 03. 2020 12:52
Re: Kruhový děj
↑ Kája2:
Ano, postup je v pořádku. Já bych každopádně onu konstantu  nevolil pevně, ale pěkně bych ji protáhl celým výpočtem a nechal ji ve výsledku (s tím, že má rozměr
nevolil pevně, ale pěkně bych ji protáhl celým výpočtem a nechal ji ve výsledku (s tím, že má rozměr  a ať se s tím každý popere jak umí). Možná to vypadá hnidopišsky, ale podobné věci bych pod koberec nezametal. Rozměry jsou základ.
a ať se s tím každý popere jak umí). Možná to vypadá hnidopišsky, ale podobné věci bych pod koberec nezametal. Rozměry jsou základ.
Offline
#13 31. 03. 2020 17:02
Re: Kruhový děj
LukasM napsal(a):
Možná to vypadá hnidopišsky, ale podobné věci bych pod koberec nezametal. Rozměry jsou základ.
Je to samozřejmě pravda a ve fundamentálních vztazích by měly být také fundamentální konstanty (u kterých rozměr každý zná).
Ale v takových těch aplikovaných vztazích (jako jsou třeba interpolace polynomem nějaké závislosti) se na to dost často kašle, protože ty rozměry stejně nepředstavují nic fyzikálního....třeba pro platinový teploměr se používá (v určitém rozsahu teplot) korekční polynom tvaru![kopírovat do textarea $R_t = R_0[1 + At +Bt^2 +C(t-100)t^3]$](/mathtex/5e/5ef03c0fa337e618b525f4e6361774c8.gif)
Kde


A úplně běžně se ten vztah udává i bez těch jednotek, které, jak sám určitě uznáš, vypadají beztak dost divně ... jen se musí uvést, že hodnota teploty v korekčním polynomu se musí dosazovat ve °C.
Pro termočlánky se používá polynom 12. stupně ... to už by z toho člověk zblbnul, kdyby měk ke všemu psát příslušnou jednotku ... stejně by to jen málokdo dokázal převést na nějakou jinou stupnici teploty...(myslím z hlavy).
Zajímavá věc je třeba vztah typu 
Argument funkce by měl být obecně bezrozměrný, ale zrovna u toho logaritmu to lze takto rozložit, a pak máme přímo logaritmus z voltů, a nikomu to nevadí...
Offline
#14 31. 03. 2020 17:17
Re: Kruhový děj
MichalAld napsal(a):
Ale v takových těch aplikovaných vztazích (jako jsou třeba interpolace polynomem nějaké závislosti) se na to dost často kašle
To já samozřejmě vím. Ale u takových vztahů skutečně musí být uvedené, v jakých jednotkách se tam tedy má dosazovat a v jakých to vyjde (z toho také už vyplynou hodnoty těch konstant). A to jsem si tady nevšiml.
Argument funkce by měl být obecně bezrozměrný, ale zrovna u toho logaritmu to lze takto rozložit, a pak máme přímo logaritmus z voltů, a nikomu to nevadí...
Mně to třeba vadí. Při číselném dosazování nevím, co mám dělat. Ano, když dosadím oboje ve stejných jednotkách, tak to vyjde stejně. Ale při prvním pohledu na vzorec nemusím poznat, že to vzniklo takhle. A také tím přijdu o možnost kontrolovat si své úpravy kontrolou jednotek.
Offline
#15 31. 03. 2020 17:45
Re: Kruhový děj
LukasM napsal(a):
Argument funkce by měl být obecně bezrozměrný, ale zrovna u toho logaritmu to lze takto rozložit, a pak máme přímo logaritmus z voltů, a nikomu to nevadí...
Mně to třeba vadí. Při číselném dosazování nevím, co mám dělat. Ano, když dosadím oboje ve stejných jednotkách, tak to vyjde stejně. Ale při prvním pohledu na vzorec nemusím poznat, že to vzniklo takhle. A také tím přijdu o možnost kontrolovat si své úpravy kontrolou jednotek.
Já jsem z toho taky vždycky vyděšený ... na druhou stranu, do toho zlomku se to taky musí dosazovat ve stejných jednotkách (přitom je jedno, v jakých)
Offline
#16 31. 03. 2020 19:06
Re: Kruhový děj
MichalAld napsal(a):
do toho zlomku se to taky musí dosazovat ve stejných jednotkách (přitom je jedno, v jakých)
Akorát že když to náhodou dosadíš v jiných a důsledně si je tam píšeš, tak najednou počítáš logaritmus něčeho, co má rozměr. A to tě zastaví. Ty jednotky si samy řeknou o to, abys s nimi něco dělal. Tj. 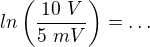 .
.
Offline
#18 01. 04. 2020 08:10
Re: Kruhový děj
↑ MichalAld:
Dobrý den,
my právě máme ve skriptech 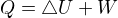 a na internetu jsme našel obě varianty.
a na internetu jsme našel obě varianty.
Offline
#20 02. 04. 2020 19:39 — Editoval Kája2 (02. 04. 2020 19:39)
Re: Kruhový děj
Dobrý večer,
reaguji ještě na předešlé reakce. Ve skriptech máme vskutku 1. termodynamicky zákon ve tvaru 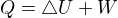 , ovšem koukal jsem i do jiné literatury a tam je to takto
, ovšem koukal jsem i do jiné literatury a tam je to takto 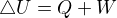 .Ve svém původním výsledku bych jen přehodil znaménko u práce. Ovšem nyní jsem tedy zmaten, jak počítat další příklady, zda se držet studijního textu či nikoliv (co se týče matematického zápisu 1.TDZ)?
.Ve svém původním výsledku bych jen přehodil znaménko u práce. Ovšem nyní jsem tedy zmaten, jak počítat další příklady, zda se držet studijního textu či nikoliv (co se týče matematického zápisu 1.TDZ)?
Offline
#21 03. 04. 2020 08:03
Re: Kruhový děj
↑ Kája2:
Toto je opravdu v každé učebnici jinak a je to tím, že každý těmi symboly značí něco jiného. Např. pokud je  přijaté plynem a W práce vykonaná vnějšími silami, tak se 1.PT vyjádří rovnicí
přijaté plynem a W práce vykonaná vnějšími silami, tak se 1.PT vyjádří rovnicí 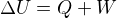 . Ale když se dohodneme, že
. Ale když se dohodneme, že  bude značit práci vykonanou tím plynem, tak u něj pak bude záporné znaménko.
bude značit práci vykonanou tím plynem, tak u něj pak bude záporné znaménko.
Ve svém příspěvku #6 počítáš práci integrálem z  , takže je to práce, vykonaná tím plynem.
, takže je to práce, vykonaná tím plynem.  značí teplo, které plyn přijal. Takže musí platit, že
značí teplo, které plyn přijal. Takže musí platit, že 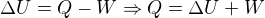 .
.
Obecně je nejlepší si ten vztah nepamatovat, ale pamatovat si jen princip. Pak ho vždy napíšeš s těmi znaménky, jaká potřebuješ.
Offline

 a změnu teploty bych spočítal tedy takto
a změnu teploty bych spočítal tedy takto  a následně teplo
a následně teplo 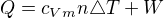 ?Tudíž celkově
?Tudíž celkově 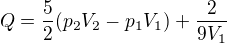 , když vezmu, že
, když vezmu, že 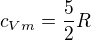 a dosadím vypočteny integrál?
a dosadím vypočteny integrál?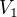 . Sčítáš tam jablka a hrušky.
. Sčítáš tam jablka a hrušky.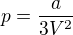 , kde
, kde