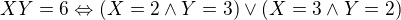Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 04. 2020 15:55
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
kovariancia
Ahojte, chcel by som este vypocitat kovarianciu, pricom tiez pojde o priklad, ktory som zverejnil tu: https://forum.matweb.cz/viewtopic.php?id=107450
kovariancia sa pocita podla vzorca ![kopírovat do textarea $cov(X,Y)=E[(X-E(X).Y-E(Y)]$](/mathtex/c0/c02eec538d41c1e10992d4408ce95a46.gif)
Ak sa nemylim tak 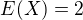
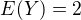
a dalej neviem ako na to ... neviem aku hodnotu v tomto pripade dosadit za "X" a "Y" vo vyssie uvedenom vzorci. Poradi mi prosim vas niekto?
Offline
#3 07. 04. 2020 16:18 — Editoval statistika_je_naj (07. 04. 2020 16:19)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
no ... takze .. ak spravne rozumiem tak ..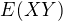 je vlastne toto? -
je vlastne toto? - 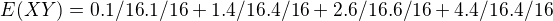 ? bojim sa ze to mam asi zle.
? bojim sa ze to mam asi zle.
Offline
#5 07. 04. 2020 16:23
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
aha .. takze musim vynasobit vsetky hodnoty z X-ka teda 0,1,2,3,4 so vsetkymi hodnotami z Y teda tiez 0,1,2,3,4?
Offline
#6 07. 04. 2020 16:27 — Editoval statistika_je_naj (07. 04. 2020 16:27)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
Myslim ze to bude takto: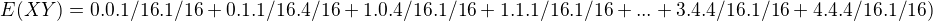
spravne?
Offline
#7 07. 04. 2020 16:29 — Editoval jarrro (07. 04. 2020 16:29)
Re: kovariancia
↑ statistika_je_naj:áno a zistiť s akou pravdepodobnosťou sa nadobúda napr.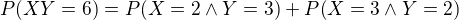
MATH IS THE BEST!!!
Offline
#8 07. 04. 2020 16:33 — Editoval statistika_je_naj (07. 04. 2020 16:34)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
uz mi vyslo 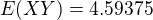
a na co je to potrebne zistit?
takze 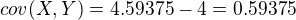
odkial vieme toto: 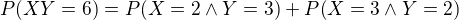 , tomu nerozumiem
, tomu nerozumiem
Offline
#9 07. 04. 2020 16:49 — Editoval jarrro (07. 04. 2020 16:59)
Re: kovariancia
↑ statistika_je_naj:Veľa tych súcinov v našom prípade bude mať nulovú pravdepodobnosť (predtým som si to neuvedomil, resp. som písal vo všeobecnosti, lebo napr. Pre súčin bodov na kockách by sa museli uvažovať všetky súčiny) teda reálne (s kladnou pravdepodobnosťou ) sa nadobudne len 0(=0*4), 3(=1*3), 4(=2*2)
Teda 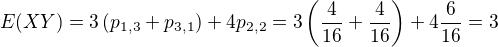
MATH IS THE BEST!!!
Offline
#10 07. 04. 2020 16:50
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
ja som to nahadzal do kalkulacky a vysiel mi vysledok takze pohoda ale skor by som sa chcel este opytat na toto: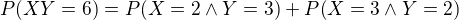
vobec totiz neviem odkial ste to odvodili
Offline
#11 07. 04. 2020 16:51
Offline
#12 07. 04. 2020 16:52
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
to ze su disjuntkne by som aj chapal ... ale ako vieme ze to P(XY=6) sa rovna tomu vyrazu napravo? to uz mi jasne nie je
Offline
#14 07. 04. 2020 17:04 — Editoval statistika_je_naj (07. 04. 2020 17:11)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
sorry ale stale nechapem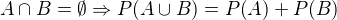
a preto plati ze 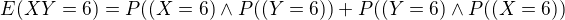 ? Nevidim tam spojitost.
? Nevidim tam spojitost.
vam to vyslo 3, mne to vyslo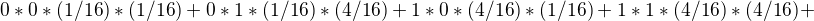
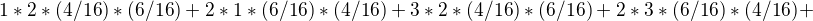
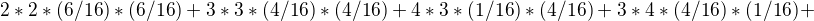
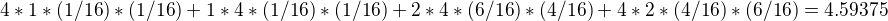 kde je chyba?
kde je chyba?
Offline
#16 07. 04. 2020 17:11
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
ja si neviem predstavit co presne znamena to "XY=6" ostatnemu rozumiem ...
Offline
#17 07. 04. 2020 17:12
Re: kovariancia
↑ statistika_je_naj:chyba je v tom, že ten výraz nevyjadruje strednú hodnotu súčinu XY
MATH IS THE BEST!!!
Offline
#18 07. 04. 2020 17:13
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
jarrro napsal(a):
↑ statistika_je_naj:chyba je v tom, že ten výraz nevyjadruje strednú hodnotu súčinu XY
tak ja neviem potom ako vyjadrit E(XY) teraz som sa uz uplne stratil
Offline
#19 07. 04. 2020 17:15
Re: kovariancia
↑ statistika_je_naj:XY=6 znamená, že súčin X a Y rovná sa 6 teda(v tvojom prípade), že súčin počtu dievčat a počtu chlapcov je 6
MATH IS THE BEST!!!
Offline
#20 07. 04. 2020 17:16
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
aha .. no stale nechapem ako urobit vypocet
E(XY)= ...
Offline
#21 07. 04. 2020 17:22 — Editoval jarrro (09. 04. 2020 11:33)
Re: kovariancia
↑ statistika_je_naj:napríklad 0 (aj ked je to jedno lebo 0* hocičo je 0) sa nadobúda s pravdepodobnosťou 2/16 a nie 1/16*1/16 1 sa nadobúda s pravdepodobnosťou 0 a nie 4/16*4/16 , 2 sa nadobúda s pravdepodobnosťou 0 a nie s takou ako si napísal atď.
Sám si zistil v minulej téme, že nie sú nezávislé tak prečo sa správaš ako keby nezávislé boli?
MATH IS THE BEST!!!
Offline
#22 07. 04. 2020 17:28 — Editoval statistika_je_naj (07. 04. 2020 17:32) Příspěvek uživatele statistika_je_naj byl skryt uživatelem statistika_je_naj. Důvod: zle
#23 07. 04. 2020 17:35
Offline
#24 07. 04. 2020 17:36 Příspěvek uživatele statistika_je_naj byl skryt uživatelem statistika_je_naj. Důvod: zle
#25 07. 04. 2020 18:00 — Editoval statistika_je_naj (07. 04. 2020 18:01)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
myslim ze uz chapem
XY=0 su dve moznosti, konkretne
BBBB
GGGG
XY=1 neexistuje ziadna moznost
XY=2 neexistuje ziadna moznost
XY=3 , to je vtedy ked x=3 a y = 1 alebo y=3 a x=1 teda su to tieto moznosti
BBBG GGGB
BBGB GGBG
BGBB GBGG
GBBB BGGG
Celkom 8 moznosti, teda 8/16 dalej
XY=4 , to je vtedy ked x=2 a y=2, to su moznosti
BBGG
BGBG
GBBG
GGBB
BGGB
GBGB
teda 6 moznosti , co je 6/16
XY=5 neexistuje ziadna moznost
XY=6 neexistuje ziadna moznost
a uz pre vyssie hodnoty neexistuje ziadna moznost
ale takto mi to vychadza len 6/16 + 8/16 = 14/16 a to je zle. Preco este musime vynasobit tych 8/16 cislom 3 a tie 6/16 cislom 4? To jedine nechapem, inac je mi to uz celkom jasne.
Offline

![kopírovat do textarea $\mathrm{cov}{\(X,Y\)}=E[\(X-E(X)\)\(Y-E(Y)\)]$](/mathtex/5b/5bc528171ca8fd8350979427331e9681.gif)
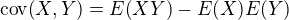
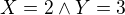 a
a 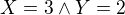 sú disjunktné
sú disjunktné