Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 04. 2020 16:11 — Editoval statistika_je_naj (23. 04. 2020 16:12)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
1000 krat hodime kockou
Ahojte mam ulohu ktoru neviem riesit a potreboval by som pomoc. Zadanie je taketo: 1000 krat hodime kockou.
Aka je pravdepodobnost ze cislo 6 padne v intervale (100,500) ? Aproximujte normalnym rozdelenim.
Kedze mam pouzit normalne rozdelenie tak som pouzil vztah pre aproximaciu binomickeho rozdelenia normalnym:
teda dostavam ze: 
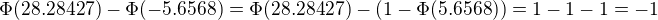
Tie hodnoty v tych 28 a 5,6 som nasiel v tabulke pre normalne rozdelenie a su to hodnoty blizke cislu 1, tak som to zaokruhlil. Prosim poradte kde mam chybu, neviem ju najst, uz som z toho zufaly.
Offline
#2 23. 04. 2020 17:10
Offline
#3 23. 04. 2020 17:31
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: 1000 krat hodime kockou
moze byt ale stale je to blbost .. ta pravdepodobnost nemoze byt ani -1 ani 1
Offline
#4 23. 04. 2020 17:37
Offline
#6 23. 04. 2020 17:39
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: 1000 krat hodime kockou
urcite nie ... ta plocha od 100 do 500 tvori tak "od oka" cca 45 %
Offline
#7 23. 04. 2020 17:50
Re: 1000 krat hodime kockou
↑ statistika_je_naj:čo vlastne počítaš ? Lebo formulácia "číslo 6 padne v intervale (100,500)" môže znamenať ,že 100 až 500 krát padne 6. čo si vypočítal správne a je to veľmi blízko k 1.
A tiež to môže znamenať aj, že 6 padne v aspoň jednom hode s poradím 100 až 500
A tiež aj že práve v tých hodoch padne a tiež aj všeliako inak a každá alternaťiva má inú odpoveď.
MATH IS THE BEST!!!
Offline
#8 23. 04. 2020 18:10 — Editoval statistika_je_naj (23. 04. 2020 18:12)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: 1000 krat hodime kockou
zo 100 hodov padne x krat cislo 6, pricom x je z intervalu (100,500)
aka je pravdepodobnost ze x bude z toho intervalu
Offline
#9 23. 04. 2020 18:13
Re: 1000 krat hodime kockou
↑ statistika_je_naj:tak potom je to 0 resp ak miesto prvého sto má byť tisíc tak približne 1 ako si aj sám zistil
MATH IS THE BEST!!!
Offline
#10 23. 04. 2020 18:22 — Editoval statistika_je_naj (23. 04. 2020 18:25)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: 1000 krat hodime kockou
to nedava zmysel, cislo 6 moze na kocke padnut najmenej 0 krat a najviac 1000 krat, je jasne ze ked mame vypocitat pravdepodobnost ze padne x krat, pricom x patri do (100,500) tak to bude nieco menej ako polovica. Prikladam obrazok. 500 bude presne v strede, cize to bude stredna hodnota normalneho rozdelenia a ta cervena cast je len malinka cast ktora je pred cislom 100 a nepatri do toho intervalu, kedze normalne rozdelenie je symetricke tak preto hovorim ze to bude nieco menej ako polovica lebo ta cervena plocha tam nebude patrit.
keby bola pravdepodobnost 1, tak to je pravdepodobnost ze 6tka na kocke padne v intervale (0,1000), normalne rozdelenie je sice od minus nekonecno po plus nekonecne ale treba si uvedomit ze ide o aproximaciu binomickeho rozdelenia a to nie je od minus nekonecno po plus nekonecno ..
alebo sa mylim?
Offline
#12 23. 04. 2020 18:30
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: 1000 krat hodime kockou
moze padnut aj 800 krat sestka, aj 900 krat ... dokonca aj 1000 krat ... (viem, pravdepodobnost je takmer nulova ale teoreticky sa to stat moze)
Offline
#13 23. 04. 2020 18:37
Re: 1000 krat hodime kockou
Môže padnúť to je jasné bavíme sa ale o pravdepodobnosti.
aj jav s naozaj nulovou pravdepodobnosťou môže nastať. (V ľubovoľného spojitého rozdelenia majù jednoprvkové javy nulovú pravdepodobnosť a predsa nejakú hodnotu dané premenne nadobudnú)
MATH IS THE BEST!!!
Offline
#14 23. 04. 2020 18:38
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: 1000 krat hodime kockou
no ok .. ja len .. logicky - ak hadzem 1000 krat, a chcem vediet aka je pravdepodobnost, ze sestka padne od 100 krat po 500 krat, tak nie je ta pravdepodobnost blizka tej jednej polovici?
Offline
#15 23. 04. 2020 18:44
Re: 1000 krat hodime kockou
↑ statistika_je_naj:nie.
Veď si vygeneruj 1000 kráť číslo medzi 1 a 6 vratane koľko krát padne 6 a celé to niekoľkokrát zopakuj.
MATH IS THE BEST!!!
Offline
#16 23. 04. 2020 18:44 — Editoval vlado_bb (23. 04. 2020 18:45)
Re: 1000 krat hodime kockou
↑ statistika_je_naj:Samozrejme ze nie. Takmer nikdy sa nestane, za by sestka padla viac ako 500 krat. Ved citaj, co ↑ jarrro: pise.
Nemylis si to s hodom mincou? Kocka ma 6 stien, nie iba dve.
Offline
#17 23. 04. 2020 18:44 — Editoval statistika_je_naj (23. 04. 2020 18:45)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: 1000 krat hodime kockou
ked sa na vec pozriem inac - predpokladajme ze hod kockou ma normalne rozdelenie: 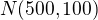
teda dostanem: a to je takmer jedna polovica.
a to je takmer jedna polovica.
tak neviem preco to nevychadza cez ten vzorec ktorym aproximujeme binomicke rozdelenie normalnym.
Offline
#18 23. 04. 2020 18:59
Re: 1000 krat hodime kockou
↑ statistika_je_naj:To limitné rozdelenie nie je 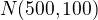 ale
ale 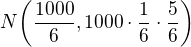
Prečo (všímam si to vo viacerých tvojich témach) najprv niečo správne zistíš a potom tie zistenia ignoruješ?
MATH IS THE BEST!!!
Offline
#19 23. 04. 2020 19:13
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: 1000 krat hodime kockou
nechapem preco je to rozdelenie 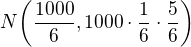 ? ako sa to rozdelenie urcuje? ja som si myslel ze ked minimum co moze sestka padnut je nula a maximum je tisic tak stredna hodnota bude priemer ..
? ako sa to rozdelenie urcuje? ja som si myslel ze ked minimum co moze sestka padnut je nula a maximum je tisic tak stredna hodnota bude priemer ..
Offline
#20 23. 04. 2020 19:20 — Editoval jarrro (23. 04. 2020 19:23)
Re: 1000 krat hodime kockou
↑ statistika_je_naj:priemer by to bol keby p=1/2 ale je 1/6 už minule som ti písal aby si nezamieňal priemer so strednou hodnotou.
a tie čísla sú preto také, lebo stredná hodnota binomického rozdelenia s parametrami 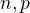 je
je 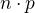 a rozptyl
a rozptyl 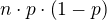
MATH IS THE BEST!!!
Offline
#21 23. 04. 2020 19:24 — Editoval statistika_je_naj (23. 04. 2020 19:29)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: 1000 krat hodime kockou
aha no jasne uz chapem ... no ok takze ... asi to nebude do 1/2, ale aj tak by to malo fungovat len jednoduchym dosadenim do vzorca
Offline
#22 23. 04. 2020 19:30
Re: 1000 krat hodime kockou
↑ statistika_je_naj:Predstav si velku nadobu, v ktorej je niekolko miliard listkov, na kazdom meno jedneho cloveka zijuceho na zemeguli. Teda aj tvoje. Tisickrat vytiahneme nejaky listok a potom ho vratime naspat a zamiesame. Kolkokrat moze byt vytiahnute tvoje meno? Samozrejme 0 az 1000 krat. Stale si myslis, ze budes vytiahnuty 500 az 1000 krat je asi tak jedna polovica?
Offline
#23 23. 04. 2020 20:14
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: 1000 krat hodime kockou
no to bude asi velmi nizka pravdepodobost .. otazka je ako to nalozit do toho vzorca s limitou v mojom prvom prispevku ..
Offline


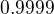 byť mohlo
byť mohlo