Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » Analytická geometrie - rovnice kružnice opsané (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 04. 2020 17:05
- nononsense

- Příspěvky: 110
- Reputace: 1
Analytická geometrie - rovnice kružnice opsané
ahoj, mám další problém. Mám zjistit rovnici kružnice opsané trojúhelníku ABC, kde![kopírovat do textarea $A=[-3,-4], B=[-2,-1], C=[1, -2]$](/mathtex/f8/f82c07ead361ba6056c681e0b6a6a751.gif)
Nevím moc, jak začít. Mám první zjistit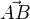 ? A z toho pak sestavit rovnici a pokračovat dál?
? A z toho pak sestavit rovnici a pokračovat dál?
Offline
- (téma jako vyřešené označil(a) nononsense)
#2 26. 04. 2020 17:19 — Editoval Ferdish (26. 04. 2020 17:20)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Analytická geometrie - rovnice kružnice opsané
Ak tie 3 body patria danej kružnici, to znamená že ich súradnice sú riešením rovnice, ktorá túto danú kružnicu definuje. Je len na tebe, či si zvolíš všeobecný alebo stredový tvar rovnice.
Každopádne do vybraného tvaru dosadíš za súradnice tých bodov a dostaneš tak sústavu troch rovníc o troch neznámych: súradnice stredu a polomer. Zvyšok sú počty.
Offline
#3 26. 04. 2020 17:24 — Editoval nejsem_tonda (26. 04. 2020 17:25)
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Analytická geometrie - rovnice kružnice opsané
↑ nononsense:
Myslim si, ze se dost vyplati mit nejaky plan. Pri planovani neresim vubec vypocty, jenom planuju, jak na sebe budou kroky navazovat.
Priklad planu:
Vim, ze stred kruznice opsane je prusecik os usecek AB, BC, CA (staci dve z nich). Takze
* spocitam rovnici osy usecky AB
* spocitam rovnici osy usecky BC
* spocitam jejich prusecik
* spocitam vzdalenost pruseciku od bodu A (protoze to je polomer hledane kruznice)
* napisu rovnici kruznice (znam jeji stred i polomer)
(V pripade, ze je nejaky krok prilis slozity, rozdelim ho na nekolik mensich kroku, tedy vytvorim "podplan".)
Jiny priklad planu:
Vim, ze rovnice libovolne kruznice vypada takto: , pricemz m, n, r jsou cisla, ktera zatim neznam. Takze
* mam tri nezname, potreboval bych tri rovnice
* kazdy z bodu A, B, C na kruznici lezi, takze kdyz tam dosadim napr. souradnice bodu A, dostanu rovnici pro neznama cisla m, n, r.
* podobne dosadim souradnice bodu B, C a dostanu dalsi dve rovnice pro neznama cisla m, n, r
* vyresim soustavu tri rovnic o trech neznamych m, n, r a tim budu vedet rovnici kruznice opsane
Vyber si jeden z planu a udelej co nejvice kroku z nej zvladnes.
Drzim palce.
Offline
#4 26. 04. 2020 17:27
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Analytická geometrie - rovnice kružnice opsané
Díky oběma. Postupoval jsem podle prvního plánu, ale asi mám někde chybu. Jestli mi to několikrát nevyjde, hodím sem můj postup. :)
Offline
#5 26. 04. 2020 17:56 — Editoval nononsense (26. 04. 2020 18:04)
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Analytická geometrie - rovnice kružnice opsané
↑ nejsem_tonda:![kopírovat do textarea $A=[-3,-4], B=[-2,-1], C=[1, -2]$](/mathtex/f8/f82c07ead361ba6056c681e0b6a6a751.gif)
Tak postupoval jsem takto: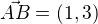


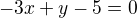



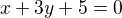
Pak jsem tedy udělal soustavu rovnic
a ta mi vyšla takto: ![kopírovat do textarea $y=-1, x=-2, P=[-2,-1]$](/mathtex/c7/c799868b21fc2424075ab651a68b1367.gif)
Teď jsem udělal vzdálenost: 
ale nevím, jestli to mám dobře, nebo jsem náhodou něco nepokazil :x
Offline
#6 26. 04. 2020 18:16
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Analytická geometrie - rovnice kružnice opsané
↑ nononsense:
Prestoze spoustu kroku je dobre, celkove to bohuzel nedava smysl.
Hodne vyrazne doporucuju zamerit na vyznam kazdeho vypoctu. U nekterych mezikroku je vyznam mozna zrejmy, ale aspon u tech "hlavnich" mezikroku fakt doporucuju si napsat / nakreslit, co jsi spocital.
Konkretne
primka prochazejici bodem A ve smeru vektoru AB (tedy primka AB zapsana parametricky)
porad primka AB, jenom zapsana v obecnem tvaru
primka BC zapsana parametricky
porad primka BC, tentokrat zapsana v obecnem tvaru
Pak jsem tedy udělal soustavu rovnic
Kdyz tem vypoctum budes prirazovat vyznamy, tak ti dojde, ze tady se pocita neco, co vubec pocitat nechceme - prusecik primek AB a BC. Neni velke prekvapeni, ze ti vyjde bod B[-2, -1].
Offline
#7 26. 04. 2020 18:44 — Editoval nononsense (26. 04. 2020 18:45)
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Analytická geometrie - rovnice kružnice opsané
↑ nejsem_tonda: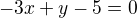
![kopírovat do textarea $S_{AB}=[-\frac{5}{2},-\frac{5}{2}]\\
-x-3y+c=0\\
c=-10$](/mathtex/8d/8d9d719cb9f29315369faeed3f5bdc72.gif)

To samé jsem udělal pro Sbc a z toho udělal soustavu dvou rovnic
Offline
#8 26. 04. 2020 18:56 Příspěvek uživatele nejsem_tonda byl skryt uživatelem nejsem_tonda. Důvod: omylem vlozeno dvakrat
#9 26. 04. 2020 19:00
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Analytická geometrie - rovnice kružnice opsané
↑ nononsense:
Jo, pak uz to budes mit cele dobre. Mimochodem jaky ma ta rovnice  vyznam? (Co jsi tim spocital?) -- Staci, kdyz si na to sam odpovis, nemusis to nutne psat verejne.
vyznam? (Co jsi tim spocital?) -- Staci, kdyz si na to sam odpovis, nemusis to nutne psat verejne.
Co byl ten klicovy dilek puzzle, kvuli kteremu jsi nevedel, jak zacit / nedopocital ses vysledku?
Offline
#10 26. 04. 2020 19:40 — Editoval nononsense (26. 04. 2020 19:43)
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Analytická geometrie - rovnice kružnice opsané
↑ nejsem_tonda:
Spočítal jsem díky tomu to "c", když jsem do ní dosadil. Ale proč se to takhle otočilo - to nevím, ale rád bych na to znal odpověď.
Hlavně mi to ještě nevyšlo. :D -> ještě jsem nedošel k výsledku. Poloměr mi vyšel 5, ale nevím jaké body dosadit za x a za y.
vím, že by to mělo být ve tvaru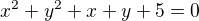
ale co mám dosadit za x a y, netuším.
Offline
#11 26. 04. 2020 19:48 — Editoval vlado_bb (26. 04. 2020 19:50)
Re: Analytická geometrie - rovnice kružnice opsané
↑ nononsense:V takom pripade je vhodne zistit a pochopit, co je rovnica kruznice (alebo vo vseobecnosti rovinnej krivky).
Alebo priamky. Napriklad - aka je rovnica priamky prechadzajucej bodmi ![kopírovat do textarea $[1,1],[2,2]$](/mathtex/dd/dde32210a6726073ea830fd5ee6d7cec.gif) ?
?
Offline
#12 26. 04. 2020 20:01
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Analytická geometrie - rovnice kružnice opsané
Hlavně mi to ještě nevyšlo. :D -> ještě jsem nedošel k výsledku. Poloměr mi vyšel 5, ale nevím jaké body dosadit za x a za y.
Tech 5 vyjde druha mocnina polomeru, takze polomer je  .
.
Ted uz znas stred kurznice: ![kopírovat do textarea $[-1;-3]$](/mathtex/14/1465a446119b14f76a1f3e7941f8f4b5.gif) a polomer. Umis z toho sestavit rovnici kruznice?
a polomer. Umis z toho sestavit rovnici kruznice?
Ono totiz pokud ne, je vlastne dost zbytecne resit tolikakrokovou ulohu, ve ktere se predpoklada, ze v tech jednotlivych krocich uz mas celkem jasno.
Ale proč se to takhle otočilo - to nevím, ale rád bych na to znal odpověď.
Kdyz na to zalozis zvlast tema "jak se odvodi rovnice primky kolme k zadane primce", tak ti tam odpovim (nebo nekdo jiny). Nema cenu tady resit tolik veci v jednom.
Offline
#13 26. 04. 2020 20:06
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Analytická geometrie - rovnice kružnice opsané
↑ vlado_bb:
x-y=0
↑ nejsem_tonda:
Aha, tak se asi podívám na google, protože ze středu a poloměru rovnici sestavit neumím. A bohužel v té knížce, kde beru příklady na to žádné cvičení není, ani o tom není zmínka.
Dobře, díky, založím na to další téma, děkuji.
Offline
#14 26. 04. 2020 20:11 — Editoval vlado_bb (26. 04. 2020 20:11)
Re: Analytická geometrie - rovnice kružnice opsané
↑ nononsense:Spravne, 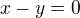 , alebo tiez
, alebo tiez  . Ak by som sa teraz opytal, co mam dosadit za
. Ak by som sa teraz opytal, co mam dosadit za  a za
a za  , davala by ti taka otazka zmysel? Lebo ty sa pytas na to iste pri kruznici.
, davala by ti taka otazka zmysel? Lebo ty sa pytas na to iste pri kruznici.
Offline
#15 26. 04. 2020 20:13 — Editoval nononsense (26. 04. 2020 20:14)
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Analytická geometrie - rovnice kružnice opsané
↑ vlado_bb:
Už jsem na to přišel! S tou kružnicí jsem to tedy pochopil a vyšlo mi to. Dosadil jsem P do vzorečku, ten jsem spočítal a došel jsem ke správnému výsledku, děkuji moc!
Offline
#16 26. 04. 2020 20:22 — Editoval nejsem_tonda (26. 04. 2020 20:24)
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Analytická geometrie - rovnice kružnice opsané
↑ nononsense:
Internet je takovy prales plny bordelu (nekvalitnich zdroju) a mezi nimi obcas narazis na velmi kvalitni zdroje. Dva takove mam ve svem podpisu.
Napriklad tady je lekce o kruznicich. Tebe ted zajima hlavne priklad cislo 2.
Offline
#17 26. 04. 2020 20:23
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Analytická geometrie - rovnice kružnice opsané
↑ nejsem_tonda:
Právě jsem narazil na jednu stránku, kde to bylo popsané, ale vskutku, všechno byl bordel a správné řešení jsem nenalezl.
Díky, podívám se na tvůj odkaz :)
Offline
#18 26. 04. 2020 20:28 — Editoval nejsem_tonda (26. 04. 2020 20:31)
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Analytická geometrie - rovnice kružnice opsané
↑ nononsense:
Samozrejme nikdy neni zaruka, ze to z toho zdroje pochopis. Strasne moc zalezi na tom, jestli mas vsechny "vstupni znalosti" a pak taky na tom, jestli je ten zpusob vysvetleni kompatibilni s tim, jak uvazuje tvuj mozek.
Ten odkaz je z ucebnice realisticky.cz, kterou doporucuju jako prvniho konzultanta prakticky na vsechno. Kdyz mas v necem mezeru, muzes se v ucebnici vratit o par kapitol zpet (kapitoly maji dokonce napsano, ktere jine kapitoly uz bys mel znat, kdyz zacinas cist).
Offline
#19 26. 04. 2020 20:34 — Editoval misaH (26. 04. 2020 20:36)
- misaH
- Příspěvky: 13438
Re: Analytická geometrie - rovnice kružnice opsané
Ahojte -
myslím, že riešenie matematických úloh je trochu aj o skúsenostiach...
Na niektoré veci je táto stránka celkom dobrá, myslím si, analogická úloha so zadaním je pod číslom 8:
https://www.priklady.eu/sk/riesene-prik … secky.alej
Offline
#20 26. 04. 2020 20:36
- nononsense

- Příspěvky: 110
- Reputace: 1
Re: Analytická geometrie - rovnice kružnice opsané
↑ nejsem_tonda:
Z tohoto tématu mám bohužel jen základy. O té kružnici jsem slyšel poprvé, v matematice jsme dost pozadu, až mě to mrzí. Teď jak se připravuji, tak jsem zjistil, že mě matika docela i baví.
Díky moc všem, odkazy si ukládám, teď se je pokusím využít při řešení ostatních úloh :)
Offline
#22 26. 04. 2020 21:13
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Analytická geometrie - rovnice kružnice opsané
↑ misaH:
Nejsem priznivcem toho tveho zdroje. Dulezitejsi je porozumet tomu, co pocitam. Pocitani do zblbnuti, dosazovani do vzorecku, kdyz jim nebudu rozumet, me ve skutecnosti moc neposune.
Ano, nejake dilci posuny prijit muzou. Muzu ziskat vetsi sebevedomi, ze to dokazu spocitat, a muzu se ve vypoctech zrychlit. Neberu ti, pokud se ti ten zdroj libi. Jenom si proste myslim, ze je to zdroj, ktery podporuje studenty v mysleni typu "ano, jste cvicene opice, po kterych se chce, aby resily nesmyslne ulohy - neni dulezite vecem rozumet, hlavne abyste to umeli spocitat".
Chapu, ze autor(ka) toho webu to urcite myslel(a) dobre. Nicmene ja takovym vecem nefandim, protoze v tom nevidim vic nez jen nacvicovani skolnich uloh.
Offline
#23 26. 04. 2020 21:53
Re: Analytická geometrie - rovnice kružnice opsané
Ahoj ↑ nononsense:,
Nezda sa ti, ze ABC je pravouhly? A to sa tu da velmi vyuzit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#24 27. 04. 2020 02:21 — Editoval misaH (27. 04. 2020 02:24)
- misaH
- Příspěvky: 13438
Re: Analytická geometrie - rovnice kružnice opsané
↑ nejsem_tonda:
Ahoj.
No - každý má právo na svoj názor.
Učím matematiku, pôvodne na strednej škole, potom na základnej.
Táto úloha je úplne jednoduchá, tak ako radí ferdish a neskôr aj vlado_bb, ktorí smerovali zadávateľa k tomu, že ak bod leží na útvare, musia jeho súradnice spĺňať rovnicu útvaru.
(Samozrejme, opísaná kružnica útvaru môže mať aj iné vlastnosti a to sa môže tiež pri riešení využiť. A ak si niekto vie všimnúť, že dané body sú vrcholy pravouhlého trojuholníka ako píše vanok, tak riešenie je ešte jednoduchšie. (Žiadne cvičené opice v tom nevidím.))
Metodicky je to tak, ako píše Vlado - najprv jednoduchšie útvary, potom zložitejšie, ale podstata je rovnaká.
Samozrejme, že treba hlavne chápať podstatu, ale tie riešené úlohy môžu ukázať akýsi prístup k špeciálnej úlohe - trebárs zrovna v tejto úlohe je naozaj jedno, ako sa postupuje (pokiaľ ide o pochopenie a logiku), ale tá všeobecná rovnica poskytuje technicky podstatne jednoduchšie, elegantnejšie riešenie ako stredová, preto som tú stránku ponúkla.
A čo komu a do akej miery vyhovuje si musí rozhodnúť on sám.
Pamätám sa - bola jediná téma, ktorú som z výkladu učiteľky na SŠ nepochopila - integrály. Internet vtedy nebol - tak som si kúpila knihu riešených úloh (doteraz ju mám) a dovtedy som sa tými riešenými úlohami prehrýzala, kým som tému nepochopila. (Vlado - vidíš, tak aj ja som sa raz v živote naučila niečo z knihy, hehe - úplne som na to zabudla...)
Keď som sa ako dieťa rozhodovala, čo pôjdem učiť, hovorila som si - čokoľvek, len nie matiku. Prečo? Veľká neistota - vyriešiš sto úloh, máš predstavu, rozumieš - a príde stoprvá úloha, a bum. Nevyriešiš, nedocvakáva... Vtedy môže riešená úloha popostrčiť, prísť vhod.
Ja tu na fóre takmer nikdy nepredkladám hotové riešenia, aj keď v tomto období nie som až taká striktná, podľa mňa vysvetľovanie žiakom samozrejme chýba. Drobná náhrada môže byť učebnica realisticky (alebo iná učebnica), ale ani tá nemusí vyhovovať všetkým, nie každému matematika chutí.
Zadávatelia by mali povinne uvádzať, čo z danej problematiky ovládajú, ináč sa zmysluplne radiť nedá.
Offline
#25 27. 04. 2020 10:07
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Analytická geometrie - rovnice kružnice opsané
↑ misaH:
Ahoj Misa,
(Samozrejme, opísaná kružnica útvaru môže mať aj iné vlastnosti a to sa môže tiež pri riešení využiť. A ak si niekto vie všimnúť, že dané body sú vrcholy pravouhlého trojuholníka ako píše vanok, tak riešenie je ešte jednoduchšie. (Žiadne cvičené opice v tom nevidím.))
Moje veta o cvicenych opicich se vztahovala k tomu zdroji, ne k teto uloze.
tá všeobecná rovnica poskytuje technicky podstatne jednoduchšie, elegantnejšie riešenie ako stredová, preto som tú stránku ponúkla
Jo s tim souhlasim, ze v teto uloze je technicky jednodussi vychazet z obecne rovnice nez ze stredove rovnice. To jsem si pri psani navrhu planu neuvedomil. Takze chapu, proc jsi ten zdroj poslala.
Nononsense si stejne nakonec vybral "svoji" cestu, takze to pro jeho reseni nehralo roli. (Technicky nejsnazsi je to, o cem pise vanok.)
Pamätám sa - bola jediná téma, ktorú som z výkladu učiteľky na SŠ nepochopila - integrály. Internet vtedy nebol - tak som si kúpila knihu riešených úloh (doteraz ju mám) a dovtedy som sa tými riešenými úlohami prehrýzala, kým som tému nepochopila. (Vlado - vidíš, tak aj ja som sa raz v živote naučila niečo z knihy, hehe - úplne som na to zabudla...)
Tak ja si dovedu predstavit velmi dobre napsanou sbirku uloh. Komentare, ktere pujdou po klicovych myslenkach, primo "na dren", nebo promyslena gradace uloh muze cloveka opravdu hodne posunout.
..., ale ani tá nemusí vyhovovať všetkým, nie každému matematika chutí.
Uplne souhlasim. Vyznamove stejny komentar jsem psal o par prispevku vyse.
Sice mam trochu jiny pohled na tvrzeni "nie kazdemu matematika chuti", ale nema asi cenu rozebirat do detailu kazdou vetu. Navic to bychom se dostali spis do filozoficke roviny a to me pres internet rozebirat nebavi.
Offline
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » Analytická geometrie - rovnice kružnice opsané (TOTO TÉMA JE VYŘEŠENÉ)