Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
Téma zavřeno
- Hlavní strana
- » Střední škola
- » Lineární nerovnice s absolutní hodnotou (TOTO TÉMA JE VYŘEŠENÉ)
#2 24. 08. 2010 13:10 — Editoval jarrro (24. 08. 2010 13:12)
Re: Lineární nerovnice s absolutní hodnotou
tu ti bolo odpovedané len je zmenený znak nerovnosti,ale postup je vždy rovnaký nulové body a riešiť na daných intervaloch
MATH IS THE BEST!!!
Offline
#4 24. 08. 2010 13:14
Re: Lineární nerovnice s absolutní hodnotou
↑ majsner:tam je zmenený zanak nerovnosti dôležitý je ten postup a ten je vždy pri nerovniciach s absolútnou hodnotou rovnaký
MATH IS THE BEST!!!
Offline
#8 24. 08. 2010 13:46
Re: Lineární nerovnice s absolutní hodnotou
↑ majsner:
První příklad:
|x|-|x-1|>0
Nulové body (to je pro jaká x nabývají výrazy s absolutní hodnotou nuly)
tedypro: x=0,x=1
Máme tedy tři intervaly:
(-oo,0),(0,1),(1,oo)
Teď vyjádříme jaké znaménka mají příslušné absolutní hodnoty na jednotlivých intervalech
Nejlépe je to dát do tabulky:
| (-oo,0) |(0,1) |(1,oo) |
---------------------------------
|x| | - | + | + |
---------------------------------
|x-1|| - | - | + |
----------------------------------
Malá pomůcka: Jakmile jednou výraz změní znaménko, už je až do konce stejné
Budeme řešit 3 nerovnice
1.pro x=(-oo,0) máme -x-(-(x-1))>0 tedy: -x+x-1>0 to neplatí pro žádné x
tak x=prázdný interval
2.pro x=(0,1) máme x-(-(x-1))>0 tedy: x+x-1>0 to platí pro x>1/2
tak x=(1/2,1)
3.pro x=(1,oo) máme x-(x-1)>0 tedy: x-x+1>0 to platí pro všechna x z daného intervalu
tak x=(1,oo)
Nyní musíme překontrolovat nulový bod 1 - dostaneme 1-(1-1)>0 - to platí.
Takže do jednoho z intervalů výsledku tu jedničku zahrneme a výsledek bude:
x=(1/2,oo)
Offline
#9 24. 08. 2010 14:11 — Editoval Rumburak (24. 08. 2010 14:12)
Re: Lineární nerovnice s absolutní hodnotou
↑ majsner:
Nerovnost  lze řešit i takto:
lze řešit i takto:
Zkouškou pro x = 0 zjistíme, že 0 nepatří do množiny jejích řešení, takže nerovnici můžeme vydělit kladným číslem |x|, při čemž znaménko
nerovnosti zůstane zachováno - dostaneme  ,
, .
.
Zde již absolutní hodnotu odstraníme velmi snadno, a sice přechodem ke složené nerovnici  , odtud dále / - 1
, odtud dále / - 1 , / *(-1)
, / *(-1) , (násobili jsme záporným číslem, čímž se obrátila znaménka nerovnosti).
, (násobili jsme záporným číslem, čímž se obrátila znaménka nerovnosti).
Z poslední nerovnosti vidíme, že x > 0 , a můžeme ji proto (beze změny znamének nerovnosti) vynásobit číslem x s výsledkem , jejíž první část je platna triviálně a z druhé části dostaneme (vydělením dvojkou)
, jejíž první část je platna triviálně a z druhé části dostaneme (vydělením dvojkou)  .
.
Offline
#10 24. 08. 2010 14:25
Re: Lineární nerovnice s absolutní hodnotou
↑ Honzc:
Zápis "x=(1/2,oo)" je zřejmě míněn dobře, ale po formální stránce jde o chybu, protože x není množinová proměnná, ale číselná proměnná
a nelze tudíž říci, že "číslo x je rovno intervalu (1/2,oo)" .
Správný zápis by byl 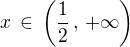 ("číslo x patří do intervalu (1/2,oo)").
("číslo x patří do intervalu (1/2,oo)").
Offline
#11 24. 08. 2010 14:31
Re: Lineární nerovnice s absolutní hodnotou
↑ Rumburak:
To já samozřejmě vím, ale protože se mi zatím nechce učit LaTex, tak nevím jak to jinak zapsat.
Offline
#12 24. 08. 2010 14:43
Re: Lineární nerovnice s absolutní hodnotou
↑ Honzc:
Jasně. Pro tazatele, který zřejmě ještě není v matematice příliš doma (čímž se ho nechci nijak dotknout) bych narhoval raději to napsat
slovy a správně, než symbolikou a špatně - pak by to třeba tak napsal do písemky a v dobré víře by si uškodil.
Offline
#13 31. 01. 2011 23:11
- Zeppelin.86

- Zelenáč
- Příspěvky: 6
- Reputace: 0
Re: Lineární nerovnice s absolutní hodnotou
Ahoj, jsem tu nováček. Peru se s jedním příkladem a jednoduše nevím, jak na něj. Vypadá takto...
Mohl by mi prosím někdo poradit, jak se dopočítat zdárného konce?
Předpokládám, že nulový bod si vypočítám z absolutní hodnoty, čili x=2 a dostanu tak dva intervaly. Pak už nevím, jak správně pokračovat dál, mate mě ten jmenovatel. Za případné rady předem děkuji!
Offline
#14 31. 01. 2011 23:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární nerovnice s absolutní hodnotou
↑ Zeppelin.86:
Zdravím,
podle pravidel je třeba založit své vlastní téma.
jelikož čitatel v zadání může být pouze nezáporný (větší nebo rovný 0), je třeba řešit pouze, kde je jimenovatel záporný. Tedy řešení nerovnice 
Stačí tak na úvod? Děkuji.
Offline
#15 29. 04. 2020 16:48
Re: Lineární nerovnice s absolutní hodnotou
Dobrý den chci se zeptat jak vypočítat tyto příklady nevím si s tím rady. Prosím kdyby bylo možné poslat i postup (krok po kroku).
Předem mockrát děkuju.
1. |x - 4| ≥ x + 2
2. |8 - x| < 3x
3. x + |2x - 1| ≤ 8
4. |7 - x| > |x + 1|
5. |x - 3| + |x + 4| ≤ x + 8
Offline
#16 29. 04. 2020 17:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární nerovnice s absolutní hodnotou
↑ vanes:
Zdravím, skoro 10 let zpět jsem napsala ↑ jelena:, že je třeba si založit vlastní téma a pořád je to třeba viz pravidla, téma si založíš z hlavní stránky kliknutím na "Založit nové téma". Do tématu si vložíš jen jednu úlohu k diskusi s kolegy (také dle pravidel), před tím ale doporučuji postudovat učebnici, kterou máš, nebo jiné materiály, např. tento a až potom se ozvat, co konkrétně není v úloze jasné.
Děkuji za pochopení.
Offline
Téma zavřeno
Stránky: 1
- Hlavní strana
- » Střední škola
- » Lineární nerovnice s absolutní hodnotou (TOTO TÉMA JE VYŘEŠENÉ)