Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 02. 05. 2020 16:26
- david_svec
- Příspěvky: 435
- Pozice: student
- Reputace: 13
Re: Množina všech reálných čísel
↑ derryos:
Zdravím,
co znamená když je exponent záporný? Vidíme, že  , co se bude s hodnotou zlomku dít, když bude x větší a větší?
, co se bude s hodnotou zlomku dít, když bude x větší a větší?
Offline
#4 02. 05. 2020 16:34
Re: Množina všech reálných čísel
↑ derryos: A pokojne mozes pouzit aj postup, ktory spominas. Z  bez problemov dostaneme
bez problemov dostaneme 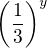 , to urcite zvladnes.
, to urcite zvladnes.
Offline
#5 02. 05. 2020 16:39
#6 02. 05. 2020 17:44 Příspěvek uživatele Ferdish byl skryt uživatelem Ferdish.
#7 02. 05. 2020 17:51
#8 02. 05. 2020 18:04
#10 02. 05. 2020 18:21
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Množina všech reálných čísel
↑ derryos:
Tím chci říct, že bys z mé nápovědy měl určit správný interval, který se nabízí v řešení.
Nic víc a nic méně.
Nikdo není dokonalý
Offline
#13 02. 05. 2020 19:02
Re: Množina všech reálných čísel
↑ derryos: Na takejto ulohe sa nic nepocita. Ak clovek chape, co je to exponencialna funkcia, tak okamzite napise odpoved, bez jedineho vypoctu.
Offline
#14 02. 05. 2020 19:16
Re: Množina všech reálných čísel
↑ vlado_bb:
můžu mít jenom otázku? Když bych si to chtěl ověřit a mám například množinu 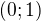 a chtěl bych dosadit například
a chtěl bych dosadit například  tak by to bylo
tak by to bylo 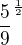 a tím pádem je to
a tím pádem je to 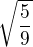 ? říkám to správně?
? říkám to správně?
Offline

 a pak
a pak  ?
?
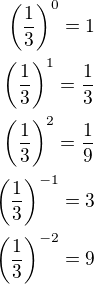

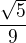 , spravne ma byt
, spravne ma byt 