Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 05. 2020 14:31
Pravděpodobnost
Zdravím,
nevím si rady s následujícím příkladem
1. Jaká je pravděpodobnost, že se spolu domluví anglicky nebo francouzsky dva náhodně vybraní hosté?
Zkoušel jsem si to rozdělit na dvě možnosti, nastane A (domluví se anglicky) nebo B (domluví se francouzsky).
S tím, že to pak sečtu (ty jevy na sobě nezávisí (že ano?))
Zkoušel jsem to i tak, že se nedomluví a tohle by byl jev opačný, ale nevycházelo mi to.
Počítal jsem to pak takto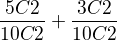 První je stav, že se domluví anglicky a druhý, že se domluví francouzsky (což je vlastně to samé jako nahoře).
První je stav, že se domluví anglicky a druhý, že se domluví francouzsky (což je vlastně to samé jako nahoře).
Ale vyšlo mi 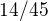 , kdežto výsledek by měl být
, kdežto výsledek by měl být  .
.
Nějaké nápady jak na to?
Děkuji!
Offline
- (téma jako vyřešené označil(a) Sikys)
#4 04. 05. 2020 16:19 — Editoval thorne (04. 05. 2020 16:22)
Re: Pravděpodobnost
↑ Sikys:
Ahoj, ty si to spočítal takhle
Ti, co mluví fra: jeden clovek plus dva, co mluví oběma jazyky
plus
Ti, co mluvím eng jsou 3 plus 2, co mluví oběma jazyky
vlastně si dvakrát započítal ty, co mluví oběma jazyky, jak psal Stýv
Takže tu dvojici stačí odečíst
Offline
#5 04. 05. 2020 16:36
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Pravděpodobnost
↑ Sikys:
Mimochodem
nastane A (domluví se anglicky) nebo B (domluví se francouzsky).
S tím, že to pak sečtu (ty jevy na sobě nezávisí (že ano?))
Naopak, jevy "domluvi se anglicky" a "domluvi se francouzsky" jsou na sobe zavisle. Staci overit, ze 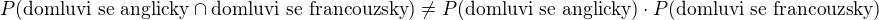
Offline
#6 04. 05. 2020 21:39 — Editoval Sikys (04. 05. 2020 21:41)
Re: Pravděpodobnost
↑ Stýv:↑ thorne:
Ok, tak jsem od toho odečetl  , což je průnik A a B. To mi vyšlo, jen nevím, jestli bych na to přišel.
, což je průnik A a B. To mi vyšlo, jen nevím, jestli bych na to přišel.
Mohl bych to vyřešit i pomocí součtu 3 jevů? To by pro mě asi bylo jednodušší...
Zkoušel jsem i takto, abych nesčítal 2krát ten průnik
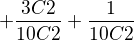
Kde 1. - Domluví se oběma jazyky
2. - Domluví se anglicky, ale ne francouzsky
3. - Domluví se francouzsky, ale ne anglicky
Nevychází mi to (dojdu k 2/15, někde je tam potřeba něco zdvojnásobit?), tak jestli byste mi mohli ještě poradit, co dělám špatně...
Snad neotravuji,
díky!
Offline
#7 04. 05. 2020 22:05 — Editoval thorne (04. 05. 2020 22:06)
Re: Pravděpodobnost
↑ Sikys:
Ahoj,
1. oběma jazyky se domluví 2 lidé, což je jedna dvojice a ne dvě
2. Takhle to můžeš také řešit a nic odčítat nebudeš, ale musíš si uvědomit, že ti, kteří se domluví oběma jazyky, se domluví i s lidmi, co umí pouze eng nebo pouze fra. Když to o tyto skupinky doplníš, tak to vyjde
3.francouzky a ne anglicky se domluví jeden člověk, takže z toho žádná dvojice nebude, 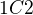 není definováno
není definováno
Neotravuješ, neboj :)
Offline