Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 05. 2020 16:38 — Editoval Mitsuko (09. 05. 2020 16:40)
Komplexní čísla - mocnina
Ahoj. Můžu poprosit o radu?
Je zadané komplexní číslo 
Mám vypočítat  , což mi vyšlo
, což mi vyšlo  .
.
Otázka zní: Nalezněte další dvě komplexní čísla, která mají stejnou třetí mocninu.
Našel jsem 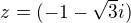 spíš tak úvahou. Jaké bude druhé komplexní číslo?
spíš tak úvahou. Jaké bude druhé komplexní číslo?
Offline
#3 09. 05. 2020 17:08
Re: Komplexní čísla - mocnina
Dalsia pomoc.
Realne cislo a, je komlexne cislo formy a+0i .
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 09. 05. 2020 17:34
Offline
#7 09. 05. 2020 23:10
Re: Komplexní čísla - mocnina
Podle mě je nejjednodušší si číslo převést na exponenciální tvar, tedy na tvar typu 
a k tomu si uvědomit, že když fázi zvýšíme o 2 PI, dostaneme pořád to samé číslo.
Když ho tedy budeme chtít umocnit na třetí, tak
tedy velikost umocníme na třetí a fázi vynásobíme třema.
A pokud teď chceme najít ta další dvě čísla, která po umocnění na třetí dají to samé, tak hledáme takovou fázi, aby nám po vynásobení 3 dala 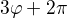 nebo
nebo 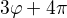 ,
,
takže zjevně původní číslo musí mít fázi 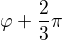 nebo
nebo  . Víc už jich není, protože další by bylo
. Víc už jich není, protože další by bylo 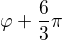 což je
což je  a to už je to samé číslo jako to se kterým jsme začli. Pokud bychom měli vyšší mocninu, bude jich více.
a to už je to samé číslo jako to se kterým jsme začli. Pokud bychom měli vyšší mocninu, bude jich více.
Offline

 ? Komplexní číslo bez imaginární části.
? Komplexní číslo bez imaginární části.