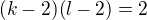Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 05. 2020 19:23 — Editoval Kája2 (16. 05. 2020 16:17)
Teorie grafů
Dobrý den,
mohu poprosit o radu k řešení toho příkladu: Určete, pro které hodnoty k,l a m je kolo 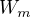 za: a.ú zároveň bipartitním grafem
za: a.ú zároveň bipartitním grafem 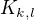 ,b.) úplným bipartitním grafem
,b.) úplným bipartitním grafem 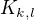 . Kolo máme definované jako graf ,, spojená z kružnice a hvězdy", který má
. Kolo máme definované jako graf ,, spojená z kružnice a hvězdy", který má  vrcholů a
vrcholů a 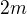 hran, kde
hran, kde 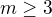 . K úloze a.) jsem si nakreslil dané grafy a bylo vidět, že pokud kolo obsahuje kružnici liché délky, pak nelze vytvořit bipartitní graf (to by plynulo i z věty, že graf bipartitní právě tehdy, když neobsahuje kružnici liché délky), tedy by platilo, že
. K úloze a.) jsem si nakreslil dané grafy a bylo vidět, že pokud kolo obsahuje kružnici liché délky, pak nelze vytvořit bipartitní graf (to by plynulo i z věty, že graf bipartitní právě tehdy, když neobsahuje kružnici liché délky), tedy by platilo, že  a
a  je sudé číslo. K otázce b.ú jsem dal do rovnosti počet vrcholů a hran:
je sudé číslo. K otázce b.ú jsem dal do rovnosti počet vrcholů a hran:  ,Odtud jsem se dostal po dání rovnic do soustavy ke vztahu
,Odtud jsem se dostal po dání rovnic do soustavy ke vztahu 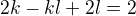 a odtud
a odtud 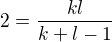 , nyní bych se snažil najít dvojice, kterým by toto vyhovalo?
, nyní bych se snažil najít dvojice, kterým by toto vyhovalo?
Offline
- (téma jako vyřešené označil(a) Kája2)
#3 16. 05. 2020 20:03
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: Teorie grafů
↑ Kája2:
Ahoj, pokud je celá úvaha správně, tak bych radši hledal celočíselná řešení rovnice 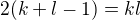 .
.
"Máte úhel beta." "No to nemám."
Offline
#4 16. 05. 2020 20:29 — Editoval Kája2 (16. 05. 2020 20:29)
Re: Teorie grafů
↑ check_drummer:
Dobrý den,
moc děkuji!Vypadá to určitě lépe.Jinak úvaha za a.) by byla správně?
Offline