Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 16. 05. 2020 19:07

cocoa
Příspěvky: 82
 

Substituční metoda pro řádově vyšší mocninovou rovnici

//forum.matweb.cz/upload3/img/2020-05/48581_Screenshot_2020-05-16%2Bbc-vzorova-prijimaci-zkouska-2014-2%2Bpdf%25281%2529.png

Dobrý den.

Použil jsem substituční metodu, abych získal prvky neznámé $x$.

$2x^{2}(x^{6}-5x^{3}+6)=0$
$x^{6}-5x^{3}+6=0$
$(x^{3})^{2}-5x^{3}+6=0$

$a=x^{3}$

$a^{2}-5a+6=0$
$(a-2)(a-3)=0$

$x^{3}=\{2, 3\}$
$x=\{\frac{1}{8}, \frac{1}{27}\}$

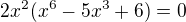
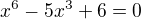
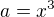
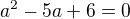
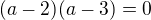
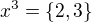
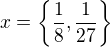
Ale patrně je to opět špatný postup.

Offline

  • (téma jako vyřešené označil(a) cocoa)

#2 16. 05. 2020 19:31 — Editoval thorne (16. 05. 2020 19:45)

thorne
Příspěvky: 108
Škola: FJFI ČVUT (od 2020)
Reputace:   3 
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

↑ cocoa:
Ahoj,
1.Pozapomněl jsi na $2x^{2}=0$
2.Áž po tohle $x^{3}=\{2, 3\}$ to je ok, ty jsi to potom špatně odmocnil $(x^{3}=2)\Rightarrow( x=\sqrt[3]{2})$

P.S.To vše za předpokladu, že$x\varepsilon \mathbb{R}$

Offline

 

#3 16. 05. 2020 20:19 — Editoval cocoa (16. 05. 2020 20:19)

cocoa
Příspěvky: 82
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

1. To jsem převedl na pravou stranu, takže: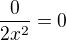

$\frac{0}{2x^{2}}=0$

Asi ne-ekvivalentní úprava, že?

2. Jo, to jsem špatně odmocnil.

Každopádně stále je podle přiloženého obrázku výsledek $c$ - což je interval.

Offline

 

#4 16. 05. 2020 20:31 — Editoval thorne (16. 05. 2020 20:32)

thorne
Příspěvky: 108
Škola: FJFI ČVUT (od 2020)
Reputace:   3 
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

↑ cocoa:
1.Udělat to můžeš, ale musíš pak zvlášť ošetřit případ$x=0$ (ve jmenovateli totiž nesmí být nula). Lepší je to nedělat a brát to jako rovnici v součinovém tvaru.

2. Tam je napsané, že kořeny té rovnice musí LEŽET v tom intervalu, výsledkem není nutně ten interval, takže c je správně, dokonce je v tom obrázku nahoře řešení :)

Offline

 

#5 16. 05. 2020 20:39

cocoa
Příspěvky: 82
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

1. Naznačil bys mi, prosím, jak bych musel ošetřit ten případ pro $x=0$? Napíšu jen podmínky, ne?

2. Nojoooo.

Offline

 

#6 16. 05. 2020 20:42 — Editoval thorne (16. 05. 2020 20:43)

thorne
Příspěvky: 108
Škola: FJFI ČVUT (od 2020)
Reputace:   3 
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

↑ cocoa:
prostě bys za x dosadil nulu do původní rovnice a spočítal to. Vyšlo by ti, že nula je také řešení.
Ale to se fakt u takových rovnic nedělá, ten součinový je lepší, alespoň mě to tak učili :)

Offline

 

#7 16. 05. 2020 21:27 — Editoval cocoa (16. 05. 2020 21:28)

cocoa
Příspěvky: 82
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

No ale pokud je $x=0$ také řešení, pak to, že jsem se k tomu nedostal, že mi vyšly 2 jiné kořeny, přece není celý výsledek, ne? To jsem se měl spíše dostat k nějakému intervalu, ne?

Offline

 

#8 16. 05. 2020 21:30

marnes
Příspěvky: 11227
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

↑ cocoa:
Řešil jsi rovnici. A řešením rovnice jsou konkrétní čísla. Interval je řešením nerovnic.

Jo. A na začátku vás zdravím.

Offline

 

#9 16. 05. 2020 21:37

cocoa
Příspěvky: 82
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

↑ marnes:

Ano, ale vyšly 2 kořeny a očividně může být i $x=0$. Takže kořeny mi nedávají všechny možné hodnoty?

Offline

 

#10 16. 05. 2020 21:44 — Editoval misaH (16. 05. 2020 21:46)

misaH
Příspěvky: 13459
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

↑ cocoa:

Ty máš vybrať pravdivé tvrdenie z predložených.

A tie tri korene naozaj ležia v intervale z odpovede c). Mmch, ak by si si tú nulu nevšimol, aj tak by odpoveď bola to c) - ak by to ale niekto opravoval, všimol by si to...

Tam nie je napísané, že riešením je celý interval.

Naozaj patria medzi -2 a 2.

Offline

 

#11 16. 05. 2020 21:46

cocoa
Příspěvky: 82
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

↑ misaH:

Jojo, to už vím, to už chápu.

Jen mě zajímají ty ostatní věci ohledně toho.

Offline

 

#12 16. 05. 2020 21:47 — Editoval thorne (16. 05. 2020 21:49)

thorne
Příspěvky: 108
Škola: FJFI ČVUT (od 2020)
Reputace:   3 
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

$2x^{2}(x^{6}-5x^{3}+6)=0$
Řešením této rovnice jsou 3 čísla $0$, $\sqrt[2]{2}$, $\sqrt[3]{2}$
Nic víc. Když si tu rovnici ve svém původním postupu vynásobil $\frac{1}{2x^{2}}$, tak si přišel o kořen x=0. To je vše.

Offline

 

#13 16. 05. 2020 22:00 — Editoval cocoa (16. 05. 2020 22:01)

cocoa
Příspěvky: 82
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

Jsem nedomýšlivec, už to vidím.

Dala by se i tato forma (Vaše zmiňovaná, bez vynásobení 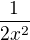$\frac{1}{2x^{2}}$) použít se substituční metodou?

...kdyby mi třeba nedošla triviální věc, že 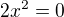$2x^{2}=0$

Offline

 

#14 16. 05. 2020 22:21 — Editoval thorne (16. 05. 2020 22:22)

thorne
Příspěvky: 108
Škola: FJFI ČVUT (od 2020)
Reputace:   3 
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

↑ cocoa:
sice moc nevím, jak to myslíš, ale tohle " $2x^{2}=0$ " by ti dojít mělo.

Offline

 

#15 16. 05. 2020 22:23

cocoa
Příspěvky: 82
 

Re: Substituční metoda pro řádově vyšší mocninovou rovnici

Jo, dává mi to větší smysl, děkuji moc, označuji za vyřešené.

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson