Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 05. 2020 14:14
nerovnice
Zdravím, potřeboval bych pomoct s touto nerovnicí, respektive s jednou úpravou/nějakou substitucí atd
ekvival. úpravami (snad) jsem došel k
A teď moc nevím, co s tím. Můžu to rozdělit na intervaly a umocnit, ale dostanu výraz s 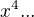 , který neumím nějak rozložit na součin (má to iracionální kořeny, rozlozit to ale jde dle pc hezky na
, který neumím nějak rozložit na součin (má to iracionální kořeny, rozlozit to ale jde dle pc hezky na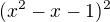 ), vhodnou substituci jsem nenašel, rozšíření
), vhodnou substituci jsem nenašel, rozšíření 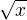 taky nic...
taky nic...
Díky
Offline
- (téma jako vyřešené označil(a) thorne)
#2 18. 05. 2020 18:13
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: nerovnice
↑ thorne:
Ahoj,
ta uprava je podle me v poradku. Ten konec podle me taky nejde udelat nejak hezceji, aby to bylo videt.
Ja akorat vim, ze kazdy polynom s realnymi koeficienty se da rozlozit na "nejhur kvadraticke zavorky" (to se s vyuzitim komplexnich cisel nahlidne rychle), takze bych zkusil
* nejdriv uhodnout racionalni koren
* potom uhodnout rozklad na dve kvadraticke zavorky
Koeficienty v tech kvadratickych zavorkach obecne nemusi byt pekne, ale kdyz budu doufat, ze by to mohly byt cela cisla, tak mam jen malo moznosti, jak ty zavorky muzou vypadat. Takze takhle bych ten rozklad na 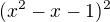 hledal.
hledal.
Offline
#3 19. 05. 2020 10:09 — Editoval thorne (19. 05. 2020 10:16)
Re: nerovnice
Díky za reakci
nejsem_tonda napsal(a):
↑ thorne:
* nejdriv uhodnout racionalni koren
* potom uhodnout rozklad na dve kvadraticke zavorky
bohužel to nemá žádné racionální kořeny, ale jde to udělat takovým tím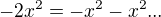 Ale kdyby to bylo něco těžšího, tak by asi šlo si napsat
Ale kdyby to bylo něco těžšího, tak by asi šlo si napsat 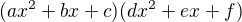 , ale dostal bych 5 rovnic o šesti neznámých a musel bych něco odhadnout (u
, ale dostal bych 5 rovnic o šesti neznámých a musel bych něco odhadnout (u 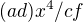 ), což je ale na h****, takže asi nic
), což je ale na h****, takže asi nic
Ale díky, označuji jako vyřešené
edit:na mobilu nemuzu dat + k reputaci :(
Offline