Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 05. 2020 08:10
- mirek_happy24

- Místo: Praha
- Příspěvky: 156
- Škola: Gymnázium Na Pražačce
- Pozice: student
- Reputace: 6
- Web
Gravitační přitažlivost dále od Země
Dobrý den, chtěl bych se zeptat na pár otázek, zde je zadání:
Korpulentní paní chce zažít ten krásný pocit, kdy poté, co se postaví na běžnou váhu, váha ukáže přijatelnou hmotnost. Proto si zaplatí cestu do vesmíru, protože ví, že větší vzdáleností od Země by si mohla své přání splnit. Jak daleko od Země musí vyletět, aby: a) hmotnost paní klesla na čtvrtinu její hmotnosti na Zemi, b)běžná váha, na kterou si paní stoupne, ukázala čtvrtinu hodnoty, kterou ukazuje na Zemi?
Přečtěte si pozorně zadání podotázek.
K výpočtu si myslím, že je třeba použít vzoreček 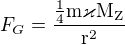
přičemž 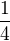 je požadovaná hmotnost paní,
je požadovaná hmotnost paní,  je hmotnost paní,
je hmotnost paní, 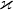 je gravitaní konstanta, hodnota
je gravitaní konstanta, hodnota 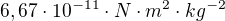
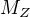 je váha Země, hodnota
je váha Země, hodnota 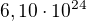 a
a  je vzdálenost paní od středu Země. ted neznámá
je vzdálenost paní od středu Země. ted neznámá
Potřeboval bych trochu poradit, jestli používám správný vzorec a správné hodnoty ,děkuji
INTELIGENTI SI ROZUMĚJÍ
Offline
- (téma jako vyřešené označil(a) mirek_happy24)
#2 22. 05. 2020 08:48
Re: Gravitační přitažlivost dále od Země
↑ mirek_happy24:
a) hmotnost je v klasické fyzike konstanta. Takže hmotnost oné paní na čtvrtinu neklesne v žádné vzdálenosti.
b) Váha měří tíhu (tj. sílu), takže ta 1/4 musí být na straně síly
na Zemi 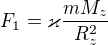
nad Zemí ve výšce  :
: 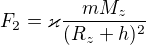
a chceš 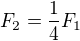
Jinak hodnoty používáš správné, ale na nic je nepotřebuješ, kromě poloměru Země.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 22. 05. 2020 10:37 — Editoval mirek_happy24 (22. 05. 2020 11:42)
- mirek_happy24

- Místo: Praha
- Příspěvky: 156
- Škola: Gymnázium Na Pražačce
- Pozice: student
- Reputace: 6
- Web
Re: Gravitační přitažlivost dále od Země
Dobrý den, podle Vaší rovnice 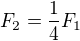 jsem dosazoval. Prosím o zkontrolování, popřípadě říct jaké mám chyby a jak to dokončit, takže:
jsem dosazoval. Prosím o zkontrolování, popřípadě říct jaké mám chyby a jak to dokončit, takže: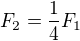
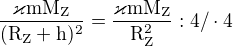
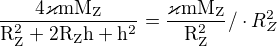
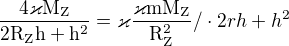
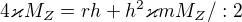
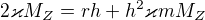
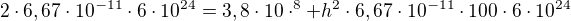
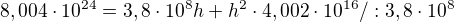
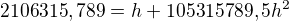
Dále nevím, předem děkuji za pomoc
INTELIGENTI SI ROZUMĚJÍ
Offline
#4 22. 05. 2020 11:31
Re: Gravitační přitažlivost dále od Země
↑ mirek_happy24:
na 2. řádku jste neměl násobit 4
na 2. řádku zkrátit 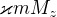
na 3. řádku je chyba
váš 4. řádek by měl ideálně být 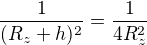
celou rovnici převrátíte, vše převedete na jednu stranu a použijete vzorec 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 22. 05. 2020 11:53
- mirek_happy24

- Místo: Praha
- Příspěvky: 156
- Škola: Gymnázium Na Pražačce
- Pozice: student
- Reputace: 6
- Web
Re: Gravitační přitažlivost dále od Země
zase jsem se zamotal, omlouvám se za neustálé otravování, snad naposled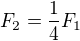
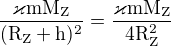
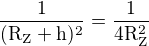
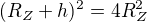
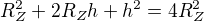
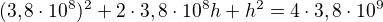
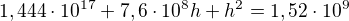
??????
INTELIGENTI SI ROZUMĚJÍ
Offline
#6 22. 05. 2020 12:04
Re: Gravitační přitažlivost dále od Země
↑ mirek_happy24:
Drsná diagnóza: máš problémy s elementární matikou.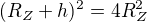
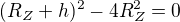
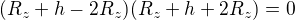
a kdy je součin nula?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 22. 05. 2020 12:06
- mirek_happy24

- Místo: Praha
- Příspěvky: 156
- Škola: Gymnázium Na Pražačce
- Pozice: student
- Reputace: 6
- Web
Re: Gravitační přitažlivost dále od Země
pardon ale takovéhle úpravy sme ještě nebrali, chodím do druhého ročníku šestiletého gymnázia
INTELIGENTI SI ROZUMĚJÍ
Offline
#8 22. 05. 2020 12:11
Re: Gravitační přitažlivost dále od Země
↑ mirek_happy24:
Aha, tak promiň.
Jenže fyzika, kterou tu řešíš není na úrovni ZŠ, takže bez té matematiky se neobejdeš.
A jestli dobře počítám, odpovídá to 9. třídě ZŠ, a tam už bys vzoreček  měl znát.
měl znát.
A stejně bys měl umět řešit kvadratickou rovnici
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#9 22. 05. 2020 13:33
- mirek_happy24

- Místo: Praha
- Příspěvky: 156
- Škola: Gymnázium Na Pražačce
- Pozice: student
- Reputace: 6
- Web
Re: Gravitační přitažlivost dále od Země
takže se to rovná buď 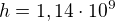 nebo
nebo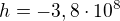
INTELIGENTI SI ROZUMĚJÍ
Offline
#10 22. 05. 2020 13:51
Re: Gravitační přitažlivost dále od Země
↑ mirek_happy24:
Ne.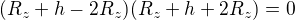
součin je nula, když aspoň jeden činitel je nula. Takže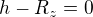 , tj.
, tj. 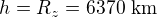
nebo 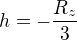 , což nedává fyzikální smysl, protže to by bylo v podzemí
, což nedává fyzikální smysl, protže to by bylo v podzemí
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#11 23. 05. 2020 11:37
Re: Gravitační přitažlivost dále od Země
Podle mě je lepší nepoužívat h (výšku nad povrchem země) ale vzdálenost od středu země.
Pokud má síla klesnout na čtvrtinu, a víme že síla klesá se čtvercem vzdálenosti ( = s druhou mocninou vzdálenosti), potom i bez dlouhého počítání musí vzdálenost od středu země vzrůst "odmocnina ze 4 krát", tedy 2x.
Online
#12 25. 05. 2020 08:53
- mirek_happy24

- Místo: Praha
- Příspěvky: 156
- Škola: Gymnázium Na Pražačce
- Pozice: student
- Reputace: 6
- Web
Re: Gravitační přitažlivost dále od Země
děkuji Vám oběma
INTELIGENTI SI ROZUMĚJÍ
Offline