Matematické Fórum

chobot161 · 22. 05. 2020 11:37

Zdravím,

dostal jsem tento úkol:

//forum.matweb.cz/upload3/img/2020-05/40162_V%25C3%25BDst%25C5%2599i%25C5%25BEek.PNG

Jak vidíte, je tam i výsledek, ale z toho vůbec nejsem chytrý.

Vůbec nevím kudy se vydat. prosím prosím o záchranu.

děkuji.

mirek_happy24 · 22. 05. 2020 11:38

podle pravidel byl jsi měl uvést aspoň svůj postup, děkuji

chobot161 · 22. 05. 2020 12:20

↑ mirek_happy24:

Ale právě o to jde, nevím jak začít :(
Napsal jsem si vzorce co jsem kolem toho našel, ale nic mi nedává smysl.

//forum.matweb.cz/upload3/img/2020-05/42786_IMG_20200522_121821.jpg

mirek_happy24 · 22. 05. 2020 12:24

z tvých vzorců je to úplně jasné, nechám tě ještě chvíli si lámat hlavu :-D

chobot161 · 22. 05. 2020 12:37

↑ mirek_happy24:

Jsem rád, že je to alespoň někomu jasné, já se s tím trápím už týden, ale jasně mi to není :D

Pořád mi v těch mých vzorcích chybí odpor :/

edison · 22. 05. 2020 17:18

Doporučuji odvodit, nebo se podívat po vzorečku pro výpočet vybíjení kondenzátoru do odporu. Ona je to taková skupina vzorců, všechny končí e^(-t/T), v drobných obměnách na všechny RC, RL a podobné obvody a vlastně se to vyskytuje i v mechanice.

Pak doporučuji za C1 a C2 udělat substituci C a ono to bude poněkud přehlednější. Až bude hotovo, vrátíš na místo C tu věc s C1 a C2.

KennyMcCormick

↑ mirek_happy24:
Já bych asi v téhle situaci zkusil napsat konkrétní radu (tj. jak to z těch vzorců vyplývá) než jenom tohle.

MichalAld · 23. 05. 2020 11:50

Pokud se nechceme moc nadřít, tak ty dva kondenzátory v sérii složíme do jednoho. Ale úplně nutné to není.

Takže už máme jen R a C v sérii. A podle nevím kolikátého Kirchoffova zákona je celkové napětí ve smyčce rovno nule (pokud neobsahuje žádné zdroje), tak můžeme napsat: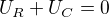

$U_R + U_C = 0$

Můžeme ovšem také psát (když kondenzátory necháme jak jsou)

$U_R + U_{C_1} + U_{C_2} = 0$

Proud musí být ve všech místech stejný (když se nám obvod nikde nevětví), takže stačí vědět, jaká je závislost mezi proudem a napětím na různých součástkách.

Pro odpor platí Ohmův zákon, tedy $u(t) = Ri(t)$ , pro kondenzátor platí $u(t) = \frac{1}{C}\int_{}^{}i(t)dt$

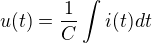
Ta malá písmena znamenají, že jde o časově proměnné veličiny (že se mění v čase).

Takže dosadíme a máme to:

$Ri(t) + \frac{1}{C}\int_{}^{}i(t)dt = 0$

Rovnice obsahující integrál se blbě řeší, takže to zderivujeme (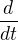 $\frac{d}{dt}$ ) a dostaneme:

$R\frac{d}{dt}i(t) + \frac{1}{C}i(t) = 0$

případně

$R\frac{d}{dt}i(t) + \frac{1}{C_1}i(t) + \frac{1}{C_2}i(t) =R\frac{d}{dt}i(t) + (\frac{1}{C_1}+\frac{1}{C_2})i(t) =0$

Diferenciální rovnici už předpokládám vyřešit umíš (jinak tu exponenciální závislost získat nelze...)

chobot161 · 24. 05. 2020 11:22

↑ MichalAld:

Mnohokrát děkuji za pomoc,

Diferenciální rovnice jsem ještě nikdy neřešil...

Ale pokusil jsem se,

Pomocí metody separace proměnných jsem se dostal sem: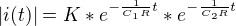

$|i(t)|=K*e^{-\frac{1}{C_{1}R}t}*e^{-\frac{1}{C_{2}R}t}$

Dál se nemůžu dostat :(

edison · 24. 05. 2020 13:52

No to je nepraktickej postup. Musíš začít substitucí za oba C a vrátit je tam až nakonec.

Jsou to prostě 2 C v sérii, chovají se jako jeden, tak je počítej jako jeden.

chobot161

↑ edison:

Dobře, zkusil jsem to tak:

$i(t)=K*e^{-\frac{1}{C R}t}$

dále jsem našel postup "úplné řešení diferenciální rovnice":

$i(t)=i(1-e^{-\frac{1}{C R}t})$
$i(t)=i+K * e^{-\frac{1}{C R}t}$
$i_{0}=i+K$
$i_{0}=0$
$K=-i$

$i(t)=i(1-e^{-\frac{1}{C R}t})$

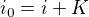
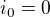
vrátil jsem tam C1 a C2 a dostal toto:

$i(t)=i(1-e^{-\frac{C_{1}+C_{2}}{C_{1}C_{2} R}t})$

To už je dost blízko výsledku, ale pořád si nejsem jistý, můžete mě zase prosím poslat správným směrem?

předem děkuji.

edison · 24. 05. 2020 20:29

chobot161 napsal(a):
$i(t)=i(1-e^{-\frac{1}{C R}t})$

Co je to i před závorkou?

Kde se vzalo 1-? (To by tam rozhodně být nemělo)

chobot161 · 24. 05. 2020 22:10

↑ edison:

čerpal jsem z tohoto podobného příkladu z reseneulohy.cz

//forum.matweb.cz/upload3/img/2020-05/50983_V%25C3%25BDst%25C5%2599i%25C5%25BEek.PNG

MichalAld · 24. 05. 2020 22:11

chobot161 napsal(a):
Pomocí metody separace proměnných jsem se dostal sem:

$|i(t)|=K*e^{-\frac{1}{C_{1}R}t}*e^{-\frac{1}{C_{2}R}t}$

Dál se nemůžu dostat :(

Jak se správně zbavit té absolutní hodnoty ti neporadím, ale nejspíš tak, že exponenciála je vždycky kladná...

Ale tohle už je správný výsledek.
$i(t)=K*e^{-\frac{1}{C_{1}R}t}*e^{-\frac{1}{C_{2}R}t}$

Když to trochu upravíme, tak z toho je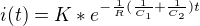

$i(t)=K*e^{-\frac{1}{R}(\frac{1}{C_1} + \frac{1}{C_2})t}$

a převést součet těch dvou zlomků 1/C1 a 1/C2 na společný jmenovatel už snad dokážeš.

chobot161 · 24. 05. 2020 22:18

↑ MichalAld:

áááno,

já moc moc děkuji, teď už to chápu,

edison · 25. 05. 2020 01:29

Poznámka: Podobný řešený příklad je pro cívku, tam je časová konstanta L/R (ty máč RC) a hlavně, tobě I začíná od max a pak se nekonečně blíží k 0, zatímco jim proud L začíná od 0 a pak se nekonečně blíží k max. Proto tam mají (1-.. a ty to tam mít nesmíš.

Matematické Fórum

#1 22. 05. 2020 11:37

Časový průběh proudu kondenzátory v sérii

#2 22. 05. 2020 11:38

Re: Časový průběh proudu kondenzátory v sérii

#3 22. 05. 2020 12:20

Re: Časový průběh proudu kondenzátory v sérii

#4 22. 05. 2020 12:24

Re: Časový průběh proudu kondenzátory v sérii

#5 22. 05. 2020 12:37

Re: Časový průběh proudu kondenzátory v sérii

#6 22. 05. 2020 17:18

Re: Časový průběh proudu kondenzátory v sérii

#7 23. 05. 2020 03:32 — Editoval KennyMcCormick (23. 05. 2020 03:40)

Re: Časový průběh proudu kondenzátory v sérii

#8 23. 05. 2020 11:50

Re: Časový průběh proudu kondenzátory v sérii

#9 24. 05. 2020 11:22

Re: Časový průběh proudu kondenzátory v sérii

#10 24. 05. 2020 13:52

Re: Časový průběh proudu kondenzátory v sérii

#11 24. 05. 2020 18:26 — Editoval chobot161 (24. 05. 2020 18:27)

Re: Časový průběh proudu kondenzátory v sérii

#12 24. 05. 2020 20:29

Re: Časový průběh proudu kondenzátory v sérii

chobot161 napsal(a):

#13 24. 05. 2020 22:10

Re: Časový průběh proudu kondenzátory v sérii

#14 24. 05. 2020 22:11

Re: Časový průběh proudu kondenzátory v sérii

chobot161 napsal(a):

#15 24. 05. 2020 22:18

Re: Časový průběh proudu kondenzátory v sérii

#16 25. 05. 2020 01:29

Re: Časový průběh proudu kondenzátory v sérii

Zápatí