Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Kvadratická rovnice s komplexními koeficienty (TOTO TÉMA JE VYŘEŠENÉ)
#1 03. 06. 2020 12:27
Kvadratická rovnice s komplexními koeficienty
Dobrý den,
maturuji tento rok z matematiky a nevím si rady s příkladem 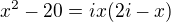 . Tento příklad je z Petákové str. 139 a výsledky mají být
. Tento příklad je z Petákové str. 139 a výsledky mají být  a
a 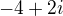 . Po úpravě jsem dostal tvar
. Po úpravě jsem dostal tvar 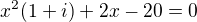 a diskriminant mi vyšel
a diskriminant mi vyšel 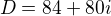 , ovšem tato metoda mi poté nevycházela, tak jsem upravil
, ovšem tato metoda mi poté nevycházela, tak jsem upravil 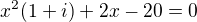 do tvaru
do tvaru 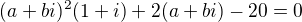 a poté jsem porovnal reálné a imaginární složky komplexního čísla
a poté jsem porovnal reálné a imaginární složky komplexního čísla 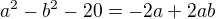 a
a 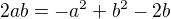 . Dostal jsem se až do tvaru
. Dostal jsem se až do tvaru 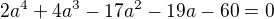 .
.
Nenapadá někoho nějaká jednodušší a rychlejší postup jak by šlo tento příklad vyřešit?
Předem děkuji.
Offline
- (téma jako vyřešené označil(a) striga)
#3 03. 06. 2020 13:31 — Editoval Rumburak (03. 06. 2020 13:32)
Re: Kvadratická rovnice s komplexními koeficienty
↑ striga:
Ähoj.
Zkusil bych upravit rovnici 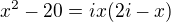 do standardního tvaru
do standardního tvaru
(1) 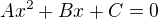 ,
,
kde  ovšem budou komplexní čísta,
ovšem budou komplexní čísta, 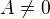 .
.
Vydělením rovnice (1) číslem  dostaneme ekvivalentní rovnici
dostaneme ekvivalentní rovnici
(2) 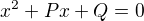 .
.
Tu pak upravíme metodou "doplnění na čverec", t.j. na tvar
(3)  .
.
Odtud  nebo
nebo 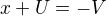 .
.
D8le snad jasné.
Offline
#4 03. 06. 2020 17:01
Re: Kvadratická rovnice s komplexními koeficienty
↑ Rumburak:
Ahoj, i tvuj postup vyzaduje vypocet odmocniny z komplexniho cisla. ktere znacis 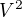 a je hodne podobny, jako kdyz resi ↑ striga: rovnici standardnim zpusobem a pocital by odmocninu z diskriminantu.
a je hodne podobny, jako kdyz resi ↑ striga: rovnici standardnim zpusobem a pocital by odmocninu z diskriminantu.
↑ striga: odmocninu z komplexniho cisla vypocitas prevodem na goniometricky tvar a pouzitim Moivreovy vety:
Offline
#7 04. 06. 2020 17:22
Re: Kvadratická rovnice s komplexními koeficienty
Poznamka.
Tu https://forum.matweb.cz/viewtopic.php?id=90346 v #9 som pripomenul jednu metodu ako a da pocitat druha od mocnina komplexneho cisla.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 05. 06. 2020 09:12 — Editoval vanok (05. 06. 2020 09:22)
Re: Kvadratická rovnice s komplexními koeficienty
Pozdravujem ↑ MichalAld:,
Poznamka.
Mas pravdu, ze niekedy pouzitie genialneho « Eulerovho vzorca » je velmi prakticke. ( tu https://en.wikipedia.org/wiki/Euler%27s_formula je o nom uzitocne citanie).
No vsak, netreba zabudnut, co sa tyka « druhej odmocniny » nenuloveho koplexneho cisla Z , ze ta koresponduje dvom rieseniam rovnice
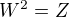 .
. Tak napr
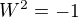 ma dve iesenia
ma dve iesenia  a
a 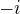 .
. ( co tiez ukazuje, ze formalne sa neda hovorit o druhej odmocnine komplexneho cisla).
Podobna poznamka plati aj pre n° odmocniny.
Inac, uz aj sredoskolak by mal ovladat aj metodu taketo vypoctu v algebrickaj forme cf. ↑ vanok:. ( a specialne ked riesi komplexne rovnice 2°, ked uz to je v osnovach strednej skoly).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Kvadratická rovnice s komplexními koeficienty (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $84+80i=4(21+2\cdot5\cdot2i)=4(5^2+2\cdot5\cdot2i+(2i)^2)=[2(5+2i)]^2$](/mathtex/31/310137693e69f3f00ff3280f8096098f.gif)
 , pak
, pak
![kopírovat do textarea $\sqrt{a+ib} = \sqrt[4]{a^2+b^2}\left(\cos\frac{\alpha}{2}+i\sin\frac{\alpha}{2}\right)$](/mathtex/68/68a5e50fc1f996265d062a12d33b49c3.gif) .
. a
a  , ziskas:
, ziskas: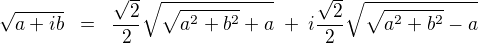
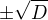 , je to jedno.
, je to jedno.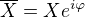 je odmocňování celkem formalita (odmocnit velikost a podělit úhel). Zase se nám to ale blbě sčítá/odčítá.
je odmocňování celkem formalita (odmocnit velikost a podělit úhel). Zase se nám to ale blbě sčítá/odčítá.