Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 08. 06. 2020 20:27
Offline
#7 09. 06. 2020 08:49
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Integrál
To záleží od substitúcie, ktorú ste aplikovala...išla ste podľa kolegu ↑ jarrro: alebo podľa kolegyne ↑ krakonoš:? Alebo ste zvolila úplne inú?
Offline
#9 09. 06. 2020 09:34
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Integrál
↑ Marcia24:
Mne sa práve rada od neho príliš nepozdáva, a to z dôvodu určenia integračných hraníc pri zavedení novej premennej. je totiž periodická funkcia a určiť jej limitu pre
je totiž periodická funkcia a určiť jej limitu pre 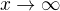 alebo
alebo  sa IMO nedá...ale možno je v tom nejaký trik.
sa IMO nedá...ale možno je v tom nejaký trik.
Offline
#11 09. 06. 2020 11:04 — Editoval laszky (09. 06. 2020 11:05)
Re: Integrál
↑ Marcia24:
Ahoj, zkus si zderivovat funkci  .
.
PS: Funguji oba dva uvedene zpusoby vypoctu.
Offline



 . Je to špatně?
. Je to špatně?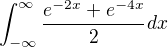
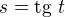 ?
? .
.