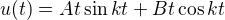Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diferenciální rovnice - fyzikální aplikace (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 06. 2020 18:38
Diferenciální rovnice - fyzikální aplikace
Dobrý den,
mohu poprosit o radu při řešení tohoto příkladu? Jedná se spíše o fyzikální aplikaci, ale jde mi o řešení. Mám naléz obecné řešení diferenciální rovnice 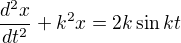 . Řešil jsem nejprve homogenní rovnici a dostal
. Řešil jsem nejprve homogenní rovnici a dostal 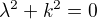 a odtud
a odtud 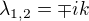 a tudiž
a tudiž 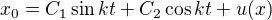 a kvůli pravé straně jsem zvolil
a kvůli pravé straně jsem zvolil 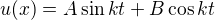 .Odtud
.Odtud  a
a  . Ovšem po dosazení do rovnice jsem dostal
. Ovšem po dosazení do rovnice jsem dostal 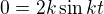 , což mi moc nesedí (nemám jak určit A aB). Mohu poprosit o radu?
, což mi moc nesedí (nemám jak určit A aB). Mohu poprosit o radu?
Offline
- (téma jako vyřešené označil(a) Kája2)
#3 09. 06. 2020 23:52
Re: Diferenciální rovnice - fyzikální aplikace
Rovnice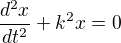
je rovnice netlumeného rezonančního obvodu (třeba LC obvod, nebo závaží na pružině) o úhlovém kmitočtu k. Pokud jej budeme budit frekvencí, která odpovídá rezonanční frekvenci, je ustálený stav nekonečno.. a pokud tedy začneme z nuly, bude výchylka pořád narůstat, takže je nutné hledat řešení ve tvaru, co zmínil ↑ laszky:
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diferenciální rovnice - fyzikální aplikace (TOTO TÉMA JE VYŘEŠENÉ)