Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 06. 2020 05:30
Gradient tlaku
Dobrý den,
prosím o radu, jak na tento příklad. Mám určit gradient vektoru tlaku v hloubce h pod hladinou kapaliny. Hustota kapaliny je 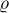 a g je tíhové zrychlení. Pro hydrostatický tlak platí
a g je tíhové zrychlení. Pro hydrostatický tlak platí  , ovšem již nevím, jak k těm parciálním derivacím. Budu rád za každou radu.
, ovšem již nevím, jak k těm parciálním derivacím. Budu rád za každou radu.
Offline
- (téma jako vyřešené označil(a) Kája2)
#6 12. 06. 2020 15:50
Re: Gradient tlaku
↑ Kája2:
Ano. S tím, že znaménko záleží na tom, jak zvolíme směr té souřadnicové osy. Pokud má platit 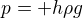 , pak je hloubka h skutečně souřadnice a prostě podle něj budeš derivovat a vyjde ti kladný výsledek (tj. zvětšuju souřadnici, roste tlak).
, pak je hloubka h skutečně souřadnice a prostě podle něj budeš derivovat a vyjde ti kladný výsledek (tj. zvětšuju souřadnici, roste tlak).
Offline
#7 13. 06. 2020 08:05
Re: Gradient tlaku
Pokud vyjádříme tlak jako funkci souřadnic, tedy  je gradient vektor, jehož složky jsou po řadě
je gradient vektor, jehož složky jsou po řadě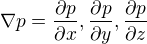
Takže celý problém spočívá v tom vyjádřit tlak jako funkci souřadnic. A před tím si musíme zvolit souřadný systém - kde bude mít počátek a jak bude natočený. A v tom máme úplně volnou ruku (přírodní zákony nezávisejí na tom, jak si zvolíme souřadný systém).
Můžeme si ho položit na hladinu tak, aby x-ová osa mířila kolmo dolů - potom bude h = x, tedy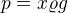
Stejně tak dobře si ho můžeme položit na hladinu osou z nahoru (a osou x třeba na sever), potom dostaneme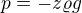
V obou případech bude mít gradient nenulovou jen jednu složku (x, nebo z), a bude rovná tomu 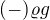
Stejně tak si ale můžeme natočit souřadný systém do obecného směru, a pak bude mít gradient nenulové všechny 3 složky.
Online
#8 13. 06. 2020 08:13
#9 13. 06. 2020 08:24
Re: Gradient tlaku
Co jsem napsal v předchozím příspěvku vypadá jednoduše, ale může se to velmi snadno zkomplikovat. Tohle by totiž platilo jen za předpokladu, že by byla Země placka, s homogenním gravitačním polem.
Takže vztah by fungoval na vesnickém rybníce, ale né na moři. Tam bychom museli vzít v úvahu kulový tvar země...takže když bychom si umístili souřadný systém přímo do středu země, byla by hloubka (R - poloměr země)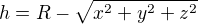
To už se nám bude derivovat mnohem veseleji.
Dále můžeme vzít také v úvahu, že gravitační zrychlení g není konstanta, nýbrž nám lineárně klesá směrem do středu země, tedy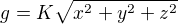
K - konstanta úměrnosti, kterou stanovíme tak, aby nám na povrchu země vyšlo g těch 9.81 (nebo kolik potřebujeme).
A to ještě pořád uvažujeme že hustota vody nezávisí na tlaku, tedy že je dokonale nestlačitelná.
Takže máme vztah
a můžeme zvesela derivovat. Případně můžeme využít toho, že pro gradient součinu dvou funkcí platí (doufám) to samé jako pro derivaci součinu dvou funkcí, tedy že 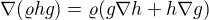
Asi každý, kdo tohle musel někdy reálně řešit ví, že mnohem lepší způsob je využít pro sféricky symetrické úlohy sférické souřadnice 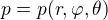 protože potom je jak hloubka tak tíhové zrychlení pouze funkcí r, a na těch směrových úhlech nezávisí. Čímž se zase dostaneme zpátky k našemu původnímu řešení.
protože potom je jak hloubka tak tíhové zrychlení pouze funkcí r, a na těch směrových úhlech nezávisí. Čímž se zase dostaneme zpátky k našemu původnímu řešení.
Online
