Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 06. 2020 22:55
Hyperbola
Zdravím, prosím jak z rovnice tečny udělat rovnici hyperboly, když vím bod dotyku? Opačný postup vím, ale do tohoto se zamotávám. Myslím že souřadnice bodu dotyku by se měly dosadit do rovnice tečny jako konstanty k x,y, ale dál jsem se nedostala.
"Když ji miluješ, je pořád co řešit..."
Offline
- (téma jako vyřešené označil(a) Kate X)
#3 15. 06. 2020 08:45
Re: Hyperbola
↑ surovec:
No má mi tam ale vyjít jeden výsledek...
"Když ji miluješ, je pořád co řešit..."
Offline
#8 15. 06. 2020 10:48
Re: Hyperbola
↑ surovec:
Je mi jasné, jak to pak vyjde, ale nechápu, jak funguje že ty čísla můžu dát do jmenovatele a mám z nich pak to a, b...
"Když ji miluješ, je pořád co řešit..."
Offline
#11 15. 06. 2020 13:37 — Editoval Cheop (15. 06. 2020 13:43)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Hyperbola
↑ Kate X:
Můžeš to počítat i takto:
Bod dotyku (4,2) dosadíš do rovnice hyperboly a dostaneš: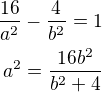
Z rovnice tečny - dosadím do hyperboly a dostanu:
- dosadím do hyperboly a dostanu: je to tečna proto diskriminant D=0
je to tečna proto diskriminant D=0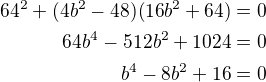 substituce
substituce 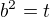
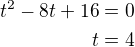 tj:
tj:
Rovnice hyperboly: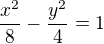
Nikdo není dokonalý
Offline


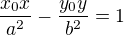 . Když dosadíme bod dotyku, máme
. Když dosadíme bod dotyku, máme . Aby absolutní člen odpovídal zadání, vynásobíme rovnici dvěma:
. Aby absolutní člen odpovídal zadání, vynásobíme rovnici dvěma: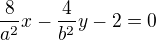 .
.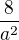 a v zadání je koeficient u x jednička (x - y - 2 = 0). Takže
a v zadání je koeficient u x jednička (x - y - 2 = 0). Takže 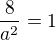 a tím pádem
a tím pádem  . Stejně pak to
. Stejně pak to  .
.