Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 23. 06. 2020 14:39
- david_svec
- Příspěvky: 435
- Pozice: student
- Reputace: 13
Re: goniometrické rovnice
↑ derryos:
Ahoj,
využij vzorec pro dvojnásobný úhel 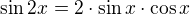 takto
takto 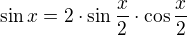 .
.
Offline
#3 23. 06. 2020 14:41
- marnes

- Příspěvky: 11227
Re: goniometrické rovnice
↑ derryos:
Zkusil bych substituci
x/2=v
sin2v nahradit 2sinvcosv
a z dvojčlenu vytknout sinv a řešit
Ale je to jen první nápad
Jo. A na začátku vás zdravím.
Offline
#5 23. 06. 2020 15:09
Re: goniometrické rovnice
↑ david_svec:
díky za odpověd ale upřímně to nedokážu dát dohromady.... mohl by si mi prosím pomoct aspoň s tím začátkem?
Offline
#6 23. 06. 2020 15:13
#10 23. 06. 2020 15:29
#11 23. 06. 2020 15:30
#12 23. 06. 2020 15:33 — Editoval vlado_bb (23. 06. 2020 15:46)
Re: goniometrické rovnice
↑ derryos: Prepac, tvoj nacrt som si (v telefone) nevsimol. Ano, 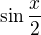 mas dobre, len si to radsej kresli iba od
mas dobre, len si to radsej kresli iba od  po
po  . No a teraz si nakreslime funkciu na pravej strane. V prvom rade - vedel by si nakreslit napriklad funkciu
. No a teraz si nakreslime funkciu na pravej strane. V prvom rade - vedel by si nakreslit napriklad funkciu 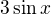 od
od  po
po  ?
?
Pripadne 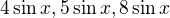 ... ide o to, aby si si uvedomil, ze na tom cisle ped sinusom nezalezi, ak nas zaujima iba POCET rieseni. Zatial jasne?
... ide o to, aby si si uvedomil, ze na tom cisle ped sinusom nezalezi, ak nas zaujima iba POCET rieseni. Zatial jasne?
Offline
#13 23. 06. 2020 15:53
Re: goniometrické rovnice
↑ vlado_bb: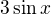 Ano to taky umím nakreslit, to bude akorát vyšší až do 3, jinak stejný. Ale moc nechápu jak se mužou tyto dvě funkce protnout, když na levý straně je kladný sinx a na pravý s mínusem (tím pádem levá funkce jde do prava a funkce na pravo jde do leva, tak jak se tedy mohou protnout?)
Ano to taky umím nakreslit, to bude akorát vyšší až do 3, jinak stejný. Ale moc nechápu jak se mužou tyto dvě funkce protnout, když na levý straně je kladný sinx a na pravý s mínusem (tím pádem levá funkce jde do prava a funkce na pravo jde do leva, tak jak se tedy mohou protnout?)
Offline
#14 23. 06. 2020 16:10 — Editoval vlado_bb (23. 06. 2020 16:11)
Re: goniometrické rovnice
↑ derryos:Aha, uz asi vidim, v com je problem. Skus sa zamysliet nad tym, ako suvisia grafy funkcii  a
a 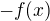 . Pokojne zacni s funkciami
. Pokojne zacni s funkciami 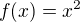 a
a 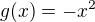 napriklad na
napriklad na ![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) .
.
Uz je to jasnejsie?
Offline
#17 23. 06. 2020 17:16
Re: goniometrické rovnice
Asi by bylo dobré aby zvládl obojí:-)
Aneb nechť do horního grafu na ↑ derryos: dokreslí ještě -sin (x/2)
Offline
#21 23. 06. 2020 17:38 — Editoval misaH (23. 06. 2020 17:41)
- misaH
- Příspěvky: 13459
Re: goniometrické rovnice
Dal si si dobrú otázku.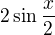 jeden hrb po 2 pí
jeden hrb po 2 pí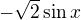 2 hrby, prvý dolu, druhý hore
2 hrby, prvý dolu, druhý hore
mal si si obidva tie grafy urobiť po 2 pí, načo 4 pí a ešte k tomu v inej mierke?
Offline
#22 23. 06. 2020 17:45
Re: goniometrické rovnice
↑ derryos:Zda sa, ze je tu viacero ludi ochotnych pomoct ti, asi by si si mohol jedneho vybrat a napisat, s kym budes dalej komunikovat, aby si tym ostatnym usetril cas. Zaroven ti odporucam - ak si uz nejakeho poradcu vyberies, ignoruj nevyziadane prispevky tych ostatnych. Inak z toho budes mat iba zmatok.
Offline
#23 23. 06. 2020 17:48 — Editoval misaH (23. 06. 2020 17:54)
- misaH
- Příspěvky: 13459
Re: goniometrické rovnice

Predsa len sa výpočtu asi nevyhneš...
A týmto končím - pohraj sa s Vladom...
Offline
#24 23. 06. 2020 18:14
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: goniometrické rovnice
↑ vlado_bb:
Ja nevim no, gulas uz v tom odpovidaci podle me davno udelali.
Prestoze bezne mam geometricky pohled na vec rad, tady bych k uloze pristupoval spis algebraicky. Staci vzit rovnici kterou napsal Cheop.
Nejaka reseni plynou z toho, ze muze nastat 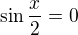 .
.
Potom se rovnice zredukuje do tvaru 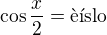 a to da nejaka dalsi reseni.
a to da nejaka dalsi reseni.
Obrazky jsou tady mirne zavadejici (pokud mi je nenakresli pocitac). Kdyby totiz rovnice vypadala treba takto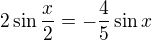
tak to pocet reseni zmeni a pritom z obrazku to moc jasne neni.
Offline
#25 23. 06. 2020 19:01
Re: goniometrické rovnice
jo takhle, takže když je před sinx mínus tak to znamená, že se jenom prohodí ty hrby (nejdřív jde dolu a pak nahoru). Já myslel že obrátí směr na levou stranu :D Teď jsem si uvědomil tu mojí blbost (ano v matice nejsem moc dobrý) :D Díky moc za rady...
Offline


 ? a funkciu
? a funkciu