Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 25. 06. 2020 21:32 Příspěvek uživatele marnes byl skryt uživatelem marnes.
#4 25. 06. 2020 21:52
Re: rovnice v C
↑ surovec:
s +1 bych to resil jako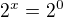
ale 2 na kolikatou je to abych vyslo -1 to nevim
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
#6 25. 06. 2020 22:07
Re: rovnice v C
↑ surovec:
ja nevim.
napadlo me to zlogaritmovat kdyby tam byla kladna 1 tak napisu x=ln(1)/ln(2)
ale opravdu nevim
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
#9 25. 06. 2020 22:24
Re: rovnice v C
↑ Meglun:
Nevím, co víš a znáš. Ale mohl bys vědět, že 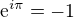 (1)
(1)
dále bys mohl vědět, že 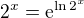
takže tvou rovnici můžeš přepsat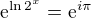
a z toho už bys měl snadno dopočítat jedno řešení.
Ale je tu malý problém, protože (1) je jen jedna z možností a obecně můžeš psát 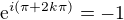 ,
, 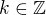 , takže obecně řešíš
, takže obecně řešíš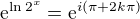
Pořádek je pro blbce, inteligent zvládá chaos!
Offline

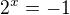
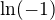 ?
?
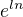 , take umim,
, take umim,